induction-heating
INDUCTION HEATING was first noted when it was found that heat was produced in transformer and motor windings, as mentioned in the Chapter “Heat Treating of Metal” in this book. Accordingly, the Principle of induction heating was studied so that motors and transformers could be built for maximum efficiency by minimizing heating losses. The develop- ment of high-frequency induction power supplies provided a means of using induction heating for surface hardening. The early use of induction involved trial and error with built-up personal knowledge of specific applications, but a lack of understanding of the basic principles. Through- out the years the understanding of the basic principles has been expanded, extending currently into computer modeling of heating applications and processes. Knowledge of these basic theories of induction heating helps to understand the application of induction heating as applied to induction heat treating. Induction heating occurs due to electromagnetic force fields producing an electrical current in a part. The parts heat due to the resis- tance to the flow of this electric current.
Resistance
All metals conduct electricity, while offering resistance to the flow of this electricity. The resistance to this flow of current causes losses in power that show up in the form of heat. This is because, according to the law of conser- vation of energy, energy is transformed from one form to another—not lost The losses produced by resistance are based upon the basic electrical formu- la: P i2R, where i is the amount of current, and R is the resistance Because the amount of loss is proportional to the square of the current, dou- bling the current significantly increases the losses (or heat) produced. Some metals, such as silver and copper, have very low resistance and, consequent-
6 / Practical Induction Heat Treating are very good conductors. Silver is expensive and is not ordinarily used
for electrical wire (although there were some induction heaters built in WorldWar II that had silver wiring because of the copper shortage). Copper wires are used to carry electricity through power lines because of the low heat losses during transmission. Other metals, such as steel, have high resis- tance to an electric current, so that when an electric current is passed through steel, substantial heat is produced. The steel heating coil on top of an electric stove is an example of heating due to the resistance to the flow of the house- hold, 60 Hz electric current. In a similar manner, the heat produced in a part in an induction coil is due to the electrical current circulating in the part.
Alternating CurrentandElectromagnetism
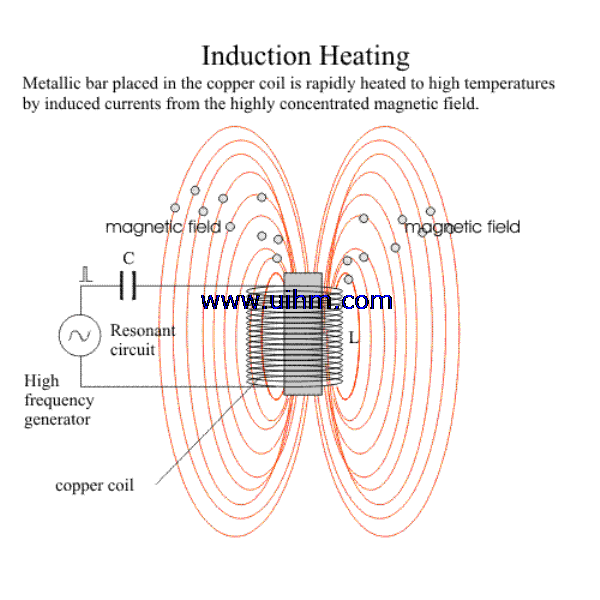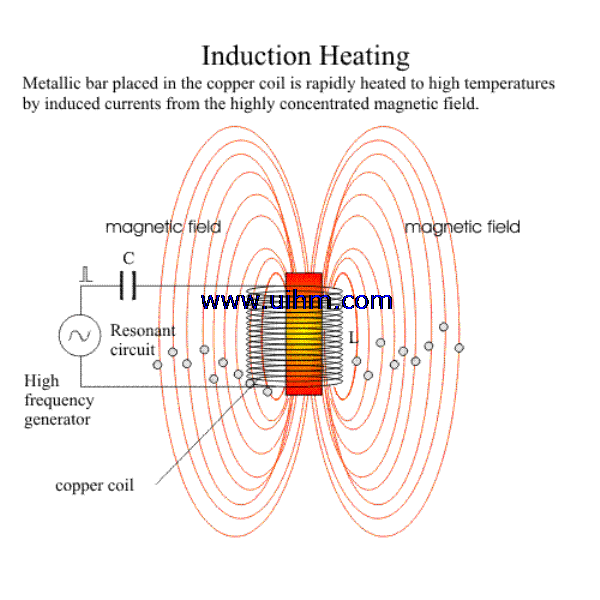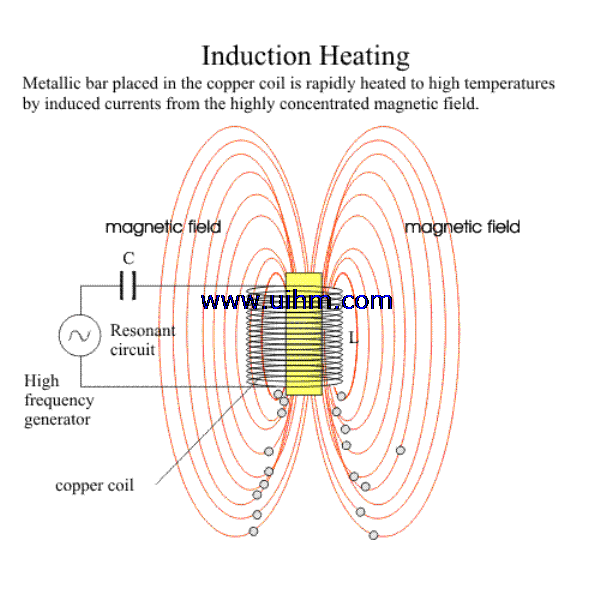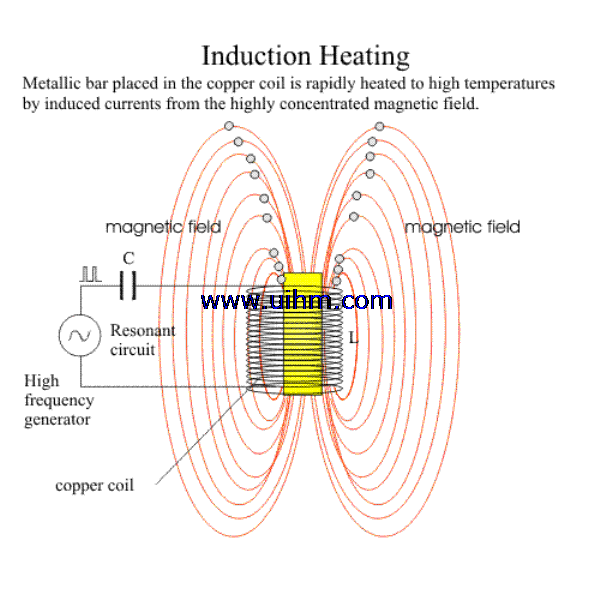
Induction heaters are used to provide alternating electric current to an elec-
tric coil (the induction coil). The induction coil becomes the electrical (heat) source that induces an electrical current into the metal part to be heated (called the workpiece). No contact is required between the workpiece and the induction coil as the heat source, and the heat is restricted to localized areas or surface zones immediately adjacent to the coil. This is because the alternating current (ac) in an induction coil has an invisible force field (elec-
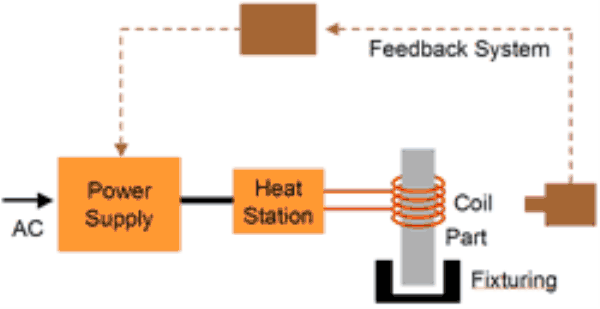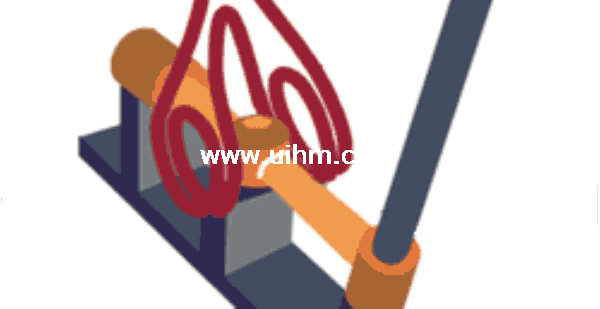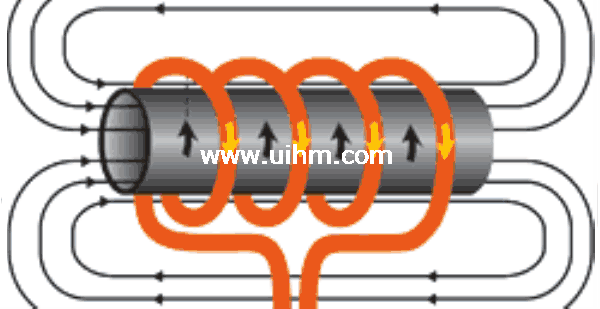
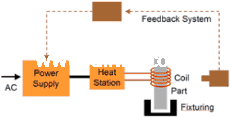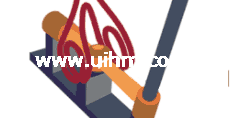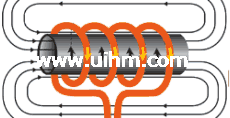
Fig. 2.1 Induction coil with electromagneticfield. OD, outside diameter; ID,
inside diameter.Source:Ref1
Theory of Heating by Induction
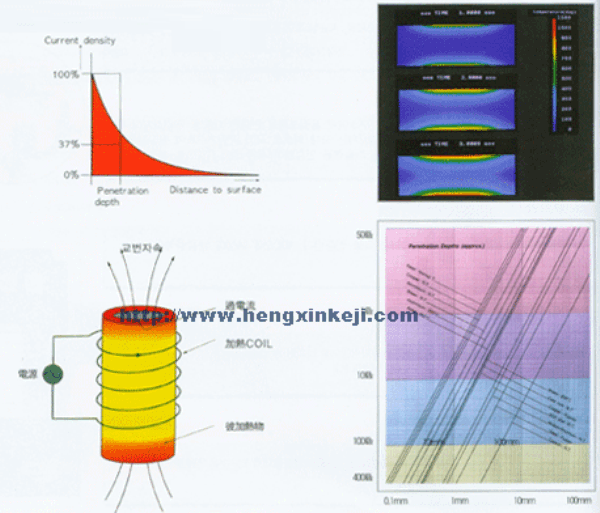
tromagnetic, or flux) around it.When the induction coil is placed next to or around a workpiece, the lines of force concentrate in the air gap between the coil and the workpiece. The induction coil actually functions as a trans- former primary, with the workpiece to be heated becoming the transformer secondary. The force field surrounding the induction coil induces an equal and opposing electric current in the workpiece, with the workpiece then heat- ing due to the resistance to the flow of this induced electric current. The rate of heating of the workpiece is dependent on the frequency of the induced current, the intensity of the induced current, the specific heat of the material, the magnetic permeability of the material, and the resistance of the material to the flow of current. Figure 2.1 shows an induction coil with the magnetic fields and induced currents produced by several coils. The induced currents are sometimes referred to as eddy-currents, with the highest intensity current being produced within the area of the intense magnetic fields.
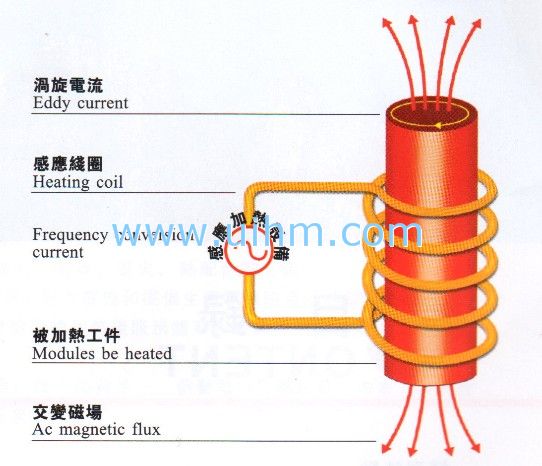
Fig. 2.2 Changein specific heat with temperaturefor materials.Source:Ref2
8 / Practical Induction Heat Treating
for various materials. Steel has the ability to absorb more heat as temperature increases. This means that more energy is required to heat steel when it is hot than when it is cold. Table 2.1 shows the difference in resistivity at room temperature between copper and steel with steel showing about ten times higher resistance than copper. At 760 °C (1400 °F) steel exhibits an increase in resistivity of about ten times larger than when at room tempera- ture. Finally, the magnetic permeability of steel is high at room temperature, but at the Curie temperature, just above 760 °C (1400 °F), steels become nonmagnetic with the effect that the permeability becomes the same as air
induction coil design
induction Principle
induction heating theory
-
Physical Characteristics:
Elementary
symbolName
Atomic weight
Specific
weightMelting point
Boiling point
Specific heat
Coefficientof
heat conductionElement
numberAg
silver
107.880
10.49
960.80
2210
0.056(0')
1.0(0'C)
47
Al
aluminum
26.97
2.699
660.2
2060
0.223
0.53
13
As
arsenic
74.91
5.73
814
610
0.082
-
33
Au
gold
197.21
9.32
1063.0
2970
0.031
0.71
79
B
boron
10.82
2.3
2300+-300
2550
0.309
-
5
Be
beryllium
9.02
1.848
1277
2770
0.52
0.038
4
Ba
barium
137.36
33.74
704+-20
1640
0.068
-
56
Bi
bismuth
209.0
9.80
271.30
1420
0.034
0.020
83
C
carbon
12.010
2.22
3700+-100
4830
0.165
0.057
6
Ca
calcium
40.8
1.55
850+-20
1440
0.149
0.30
20
Cd
cadmium
112.41
8.65
320.9
765
0.055
0.22
48
Ce
cerium
140.13
6.9
600+-50
1440
0.042
-
58
Co
cobalt
58.94
8.85
1499+-1
2900
0.099
0.165
27
Cr
chromium
52.01
77.19
1875
2500
0.11
0.16
24
Cs
cesium
132.91
1.9
28+2
690
0.052
-
55
Cu
copper
63.54
8.96
1083.0
2600
0.092
0.94
29
Fe
iron
55.85
7.896
1536.0
2740
0.11
0.18
26
Ga
gallium
69.73
5.91
29.87
2070
0.079
-
31
Ge
germanium
72.60
5.36
958+-10
2700
0.073
-
32
Hg
mercury
200.61
13.546
38.36
357
0.033
0.0201
80
In
indium
114.76
7.31
156.4
1450
0.057
0.057
49
Ir
iridium
193.1
22.5
2454+-3
5300
0.031
0.147
7
K
potassium
39.096
0.86
63.7
770
0.177
0.24
19
La
lanthaduim
138.92
6.15
826+-5
1800
0.045
-
57
Li
lithium
6.940
0.535
186+-5
1370
0.79
0.17
3
Mg
hydrogen
24.32
1.74
650+-2
1110
0.25
0.38
12
Mn
manganess
54.93
7.43
1245
2150
0.115
-
25
Mo
molybdenum
95.95
10.22
2610
3700
0.061
0.35
42
Na
sodium
22.997
0.971
92.82
892
0.295
0.32
11
Nb
niobium
92.91
8.57
2468+-10
>3300
0.065(0'C)
-
41
Ni
nickel
58.69
8.902
1453
2730
0.112
0.198
28
Os
osmium
190.2
22.5
2700+-200
5500
0.031
-
76
P
phosphorus
30.98
1.82
441
280
0.017
-
15
Pb
lead
207.21
11.36
327.4258
1740
0.031
0.08
82
Pd
palladium
106.7
12.03
1544
4000
0.058(0'C)
0.17
46
Pt
platinium
195.23
21.45
1769
4410
0.032
0.17
78
Rb
rubidium
85.48
1.53
39+-1
680
0.080
-
37
Rn
radon
102.91
12.44
1966+-3
4500
0.059
0.21
45
Ru
ruthenium
101.7
12.2
2500+-100
4900
0.057(0'C)
-
44
S
sulfer
32.066
2.07
119.0
444.6
0.175
-
16
Sb
antimony
121.76
6.62
630.5
1440
0.049
0.045
51
Se
selenium
78.96
4.81
220+-5
680
0.084
-
34
Si
selicon
28.06
2.33
1430+-20
2300
0.162(0'C)
0.20
14
Sn
tin
118.70
7.298
231.9
2270
0.054
0.16
50
Sr
strontium
87.63
2.6
770+-10
1380
0.176
-
38
Ta
tantalum
180.88
16.654
2996+-50
>4100
0.036(0'C)
0.13
73
Tc
technetium
127.61
6.235
450+-10
1390
0.047
0.014
52
Th
thorium
232.12
11.66
1750
>3000
0.126
-
22
Ti
titanium
47.90
4.507
1688+-10
>3000
0.126
-
22
Tl
thallium
204.39
11.85
300+-3
1460
0.031
0.093
81
U
uranium
238.07
19.07
1132+-5
-
0.028
0.064
92
V
vanadium
50.95
6.1
1900+25
3460
0.120
-
23
W
tungsten
183.92
19.03
3410
5930
0.032
0.48
74
Zn
zinc
65.38
7.133
419.505
906
0.0915
0.27
30
Zr
zirconium
91.22
6.489
6.489
>2900
0.066
-
40
Ohm's Law
Ohm's Law states that in a simple electrical circuit, the strength of a current (I) flowing through a resistance (R) is proportional to the applied voltage (E). It is expressed by the formula:

Thus, if you increase the voltage, and resistance remains the same, the current will increase proportionately.
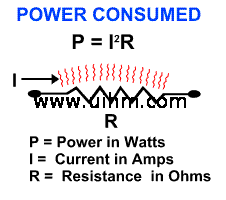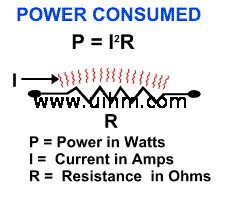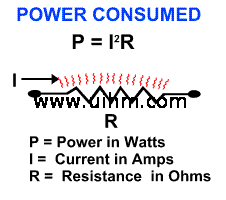
Resistive Heating
Resistance is well named, for it opposes current flow. The lower the resistance, the higher the current flow in the curcuit, and hence the greater the power. This power (P) is the rate at which electrical energy is transformed into heat. It is expressed by the formula:

This heat can be put to good purpose and is the principle behind heating elements such as you will find in hair dryers and baseboard heaters. However, such direct production of heat is inefficient, localized, and difficult to control. For industrial purposes it is preferable to produce heat by using an induced current rather than a direct one.
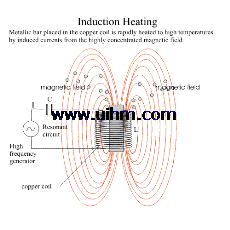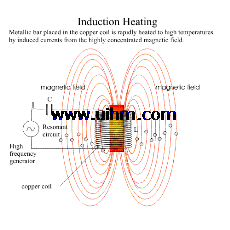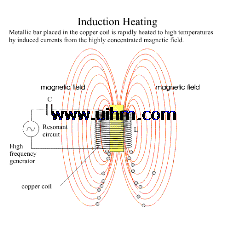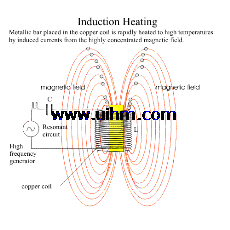
Induction Heating
With induction heating, we substitute an induced current for a direct one, which is of course the principle of the transformer. It works this way. Alternating current flowing through the primary coils of the transformer creates an electromagnetic alternating field. Since the reverse is also true, by placing secondary coils within that field, we will induce a current to flow through them. And depending on the respective number of electrical turns in the primary and the secondary, we can step up or step down the voltage levels. It is the voltage in the secondary turns which, when applied to heating elements, creates the energy to heat or melt metals.
Resistive Heating Illustrated
Induction Heating Illustrated
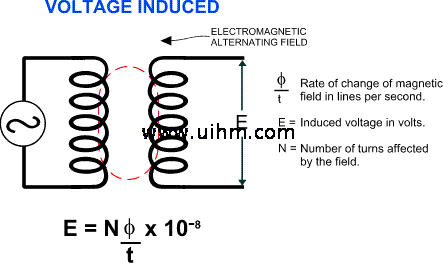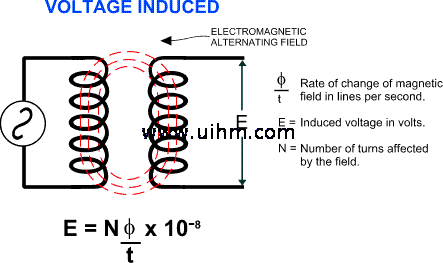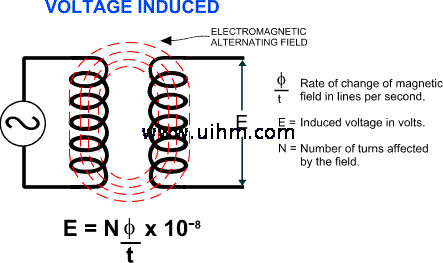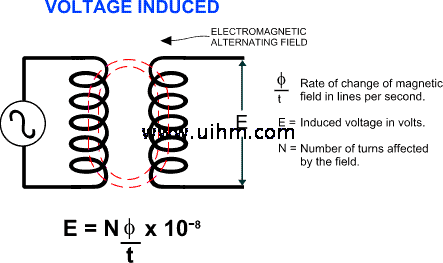
Current flow is induced in the secondary circuit by placing the secondary turns within the changing magnetic field created by the primary turns.





Newest Comment
No Comment
Post Comment