TRANSFORMERS of induction heating
Views Send Enquiry
- Mutual inductance and basic operation
- Step-up and step-down transformers
- Electrical isolation
- Phasing
- Winding configurations
- Voltage regulation
- Special transformers and applications
- Practical considerations
- Contributors
- Bibliography
Mutual inductance and basic operation
Suppose we were to wrap a coil of insulated wire around a loop of ferromagnetic material and energize this coil with an AC voltage source: (Figure below (a))

Insulated winding on ferromagnetic loop has inductive reactance, limiting AC current.
As an inductor, we would expect this iron-core coil to oppose the applied voltage with its inductive reactance, limiting current through the coil as predicted by the equations XL = 2πfL and I=E/X (or I=E/Z). For the purposes of this example, though, we need to take a more detailed look at the interactions of voltage, current, and magnetic flux in the device.
Kirchhoff's voltage law describes how the algebraic sum of all voltages in a loop must equal zero. In this example, we could apply this fundamental law of electricity to describe the respective voltages of the source and of the inductor coil. Here, as in any one-source, one-load circuit, the voltage dropped across the load must equal the voltage supplied by the source, assuming zero voltage dropped along the resistance of any connecting wires. In other words, the load (inductor coil) must produce an opposing voltage equal in magnitude to the source, in order that it may balance against the source voltage and produce an algebraic loop voltage sum of zero. From where does this opposing voltage arise? If the load were a resistor (Figure above (b)), the voltage drop originates from electrical energy loss, the “friction” of electrons flowing through the resistance. With a perfect inductor (no resistance in the coil wire), the opposing voltage comes from another mechanism: the reaction to a changing magnetic flux in the iron core. When AC current changes, flux Φ changes. Changing flux induces a counter EMF.
Michael Faraday discovered the mathematical relationship between magnetic flux (Φ) and induced voltage with this equation:

The instantaneous voltage (voltage dropped at any instant in time) across a wire coil is equal to the number of turns of that coil around the core (N) multiplied by the instantaneous rate-of-change in magnetic flux (dΦ/dt) linking with the coil. Graphed, (Figure below) this shows itself as a set of sine waves (assuming a sinusoidal voltage source), the flux wave 90o lagging behind the voltage wave:
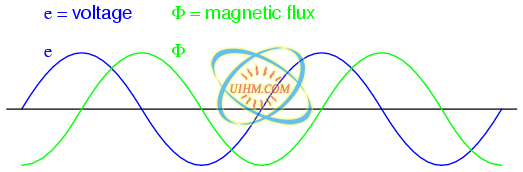
Magnetic flux lags applied voltage by 90o because flux is proportional to a rate of change, dΦ/dt.
Magnetic flux through a ferromagnetic material is analogous to current through a conductor: it must be motivated by some force in order to occur. In electric circuits, this motivating force is voltage (a.k.a. electromotive force, or EMF). In magnetic “circuits,” this motivating force is magnetomotive force, or mmf. Magnetomotive force (mmf) and magnetic flux (Φ) are related to each other by a property of magnetic materials known as reluctance (the latter quantity symbolized by a strange-looking letter “R”):

In our example, the mmf required to produce this changing magnetic flux (Φ) must be supplied by a changing current through the coil. Magnetomotive force generated by an electromagnet coil is equal to the amount of current through that coil (in amps) multiplied by the number of turns of that coil around the core (the SI unit for mmf is the amp-turn). Because the mathematical relationship between magnetic flux and mmf is directly proportional, and because the mathematical relationship between mmf and current is also directly proportional (no rates-of-change present in either equation), the current through the coil will be in-phase with the flux wave as in (Figure below)
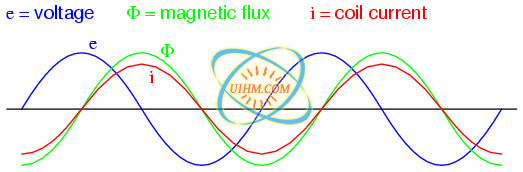
Magnetic flux, like current, lags applied voltage by 90o.
This is why alternating current through an inductor lags the applied voltage waveform by 90o: because that is what is required to produce a changing magnetic flux whose rate-of-change produces an opposing voltage in-phase with the applied voltage. Due to its function in providing magnetizing force (mmf) for the core, this current is sometimes referred to as the magnetizing current.
It should be mentioned that the current through an iron-core inductor is not perfectly sinusoidal (sine-wave shaped), due to the nonlinear B/H magnetization curve of iron. In fact, if the inductor is cheaply built, using as little iron as possible, the magnetic flux density might reach high levels (approaching saturation), resulting in a magnetizing current waveform that looks something like Figure below
As flux density approaches saturation, the magnetizing current waveform becomes distorted.
When a ferromagnetic material approaches magnetic flux saturation, disproportionately greater levels of magnetic field force (mmf) are required to deliver equal increases in magnetic field flux (Φ). Because mmf is proportional to current through the magnetizing coil (mmf = NI, where “N” is the number of turns of wire in the coil and “I” is the current through it), the large increases of mmf required to supply the needed increases in flux results in large increases in coil current. Thus, coil current increases dramatically at the peaks in order to maintain a flux waveform that isn't distorted, accounting for the bell-shaped half-cycles of the current waveform in the above plot.
The situation is further complicated by energy losses within the iron core. The effects of hysteresis and eddy currents conspire to further distort and complicate the current waveform, making it even less sinusoidal and altering its phase to be lagging slightly less than 90o behind the applied voltage waveform. This coil current resulting from the sum total of all magnetic effects in the core (dΦ/dt magnetization plus hysteresis losses, eddy current losses, etc.) is called the exciting current. The distortion of an iron-core inductor's exciting current may be minimized if it is designed for and operated at very low flux densities. Generally speaking, this requires a core with large cross-sectional area, which tends to make the inductor bulky and expensive. For the sake of simplicity, though, we'll assume that our example core is far from saturation and free from all losses, resulting in a perfectly sinusoidal exciting current.
As we've seen already in the inductors chapter, having a current waveform 90o out of phase with the voltage waveform creates a condition where power is alternately absorbed and returned to the circuit by the inductor. If the inductor is perfect (no wire resistance, no magnetic core losses, etc.), it will dissipate zero power.
Let us now consider the same inductor device, except this time with a second coil (Figure below) wrapped around the same iron core. The first coil will be labeled the primary coil, while the second will be labeled the secondary:
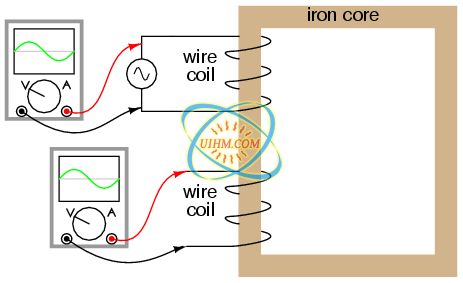
Ferromagnetic core with primary coil (AC driven) and secondary coil.
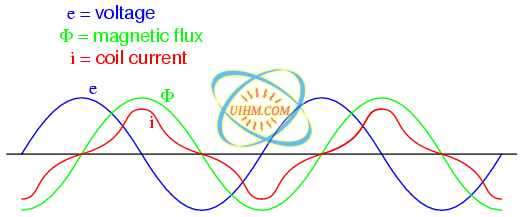
If this secondary coil experiences the same magnetic flux change as the primary (which it should, assuming perfect containment of the magnetic flux through the common core), and has the same number of turns around the core, a voltage of equal magnitude and phase to the applied voltage will be induced along its length. In the following graph, (Figure below) the induced voltage waveform is drawn slightly smaller than the source voltage waveform simply to distinguish one from the other:
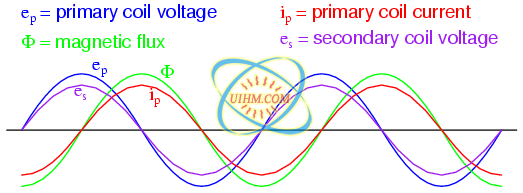
Open circuited secondary sees the same flux Φ as the primary. Therefore induced secondary voltage es is the same magnitude and phase as the primary voltage ep.
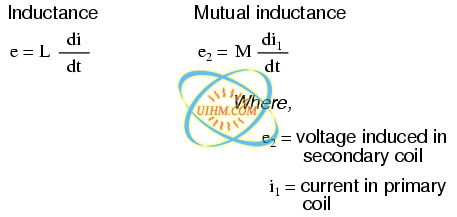
This effect is called mutual inductance: the induction of a voltage in one coil in response to a change in current in the other coil. Like normal (self-) inductance, it is measured in the unit of Henrys, but unlike normal inductance it is symbolized by the capital letter “M” rather than the letter “L”:
No current will exist in the secondary coil, since it is open-circuited. However, if we connect a load resistor to it, an alternating current will go through the coil, in-phase with the induced voltage (because the voltage across a resistor and the current through it are always in-phase with each other). (Figure below)
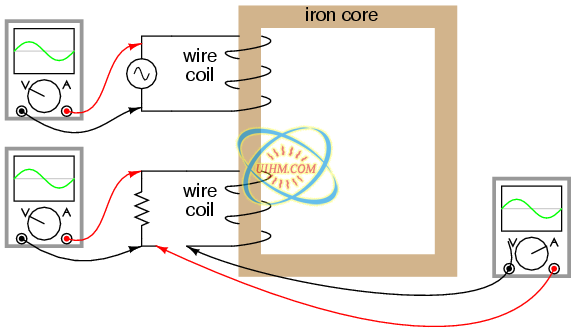
Resistive load on secondary has voltage and current in-phase.
At first, one might expect this secondary coil current to cause additional magnetic flux in the core. In fact, it does not. If more flux were induced in the core, it would cause more voltage to be induced voltage in the primary coil (remember that e = dΦ/dt). This cannot happen, because the primary coil's induced voltage must remain at the same magnitude and phase in order to balance with the applied voltage, in accordance with Kirchhoff's voltage law. Consequently, the magnetic flux in the core cannot be affected by secondary coil current. However, what does change is the amount of mmf in the magnetic circuit.
Magnetomotive force is produced any time electrons move through a wire. Usually, this mmf is accompanied by magnetic flux, in accordance with the mmf=ΦR “magnetic Ohm's Law” equation. In this case, though, additional flux is not permitted, so the only way the secondary coil's mmf may exist is if a counteracting mmf is generated by the primary coil, of equal magnitude and opposite phase. Indeed, this is what happens, an alternating current forming in the primary coil -- 180o out of phase with the secondary coil's current -- to generate this counteracting mmf and prevent additional core flux. Polarity marks and current direction arrows have been added to the illustration to clarify phase relations: (Figure below)
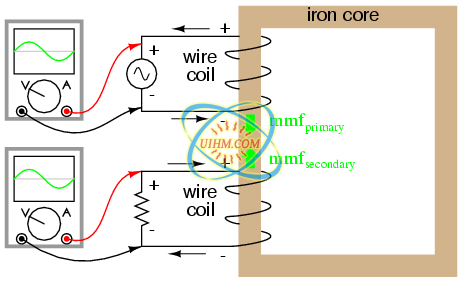
Flux remains constant with application of a load. However, a counteracting mmf is produced by the loaded secondary.
If you find this process a bit confusing, do not worry. Transformer dynamics is a complex subject. What is important to understand is this: when an AC voltage is applied to the primary coil, it creates a magnetic flux in the core, which induces AC voltage in the secondary coil in-phase with the source voltage. Any current drawn through the secondary coil to power a load induces a corresponding current in the primary coil, drawing current from the source.
Notice how the primary coil is behaving as a load with respect to the AC voltage source, and how the secondary coil is behaving as a source with respect to the resistor. Rather than energy merely being alternately absorbed and returned the primary coil circuit, energy is now being coupled to the secondary coil where it is delivered to a dissipative (energy-consuming) load. As far as the source “knows,” it's directly powering the resistor. Of course, there is also an additional primary coil current lagging the applied voltage by 90o, just enough to magnetize the core to create the necessary voltage for balancing against the source (the exciting current).
We call this type of device a transformer, because it transforms electrical energy into magnetic energy, then back into electrical energy again. Because its operation depends on electromagnetic induction between two stationary coils and a magnetic flux of changing magnitude and “polarity,” transformers are necessarily AC devices. Its schematic symbol looks like two inductors (coils) sharing the same magnetic core: (Figure below)
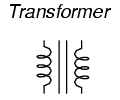
Schematic symbol for transformer consists of two inductor symbols, separated by lines indicating a ferromagnetic core.
The two inductor coils are easily distinguished in the above symbol. The pair of vertical lines represent an iron core common to both inductors. While many transformers have ferromagnetic core materials, there are some that do not, their constituent inductors being magnetically linked together through the air.
The following photograph shows a power transformer of the type used in gas-discharge lighting. Here, the two inductor coils can be clearly seen, wound around an iron core. While most transformer designs enclose the coils and core in a metal frame for protection, this particular transformer is open for viewing and so serves its illustrative purpose well: (Figure below)

Example of a gas-discharge lighting transformer.
Both coils of wire can be seen here with copper-colored varnish insulation. The top coil is larger than the bottom coil, having a greater number of “turns” around the core. In transformers, the inductor coils are often referred to as windings, in reference to the manufacturing process where wire is wound around the core material. As modeled in our initial example, the powered inductor of a transformer is called the primary winding, while the unpowered coil is called the secondary winding.
In the next photograph, Figure below, a transformer is shown cut in half, exposing the cross-section of the iron core as well as both windings. Like the transformer shown previously, this unit also utilizes primary and secondary windings of differing turn counts. The wire gauge can also be seen to differ between primary and secondary windings. The reason for this disparity in wire gauge will be made clear in the next section of this chapter. Additionally, the iron core can be seen in this photograph to be made of many thin sheets (laminations) rather than a solid piece. The reason for this will also be explained in a later section of this chapter.

Transformer cross-section cut shows core and windings.
It is easy to demonstrate simple transformer action using SPICE, setting up the primary and secondary windings of the simulated transformer as a pair of “mutual” inductors. (Figure below) The coefficient of magnetic field coupling is given at the end of the “k” line in the SPICE circuit description, this example being set very nearly at perfection (1.000). This coefficient describes how closely “linked” the two inductors are, magnetically. The better these two inductors are magnetically coupled, the more efficient the energy transfer between them should be.
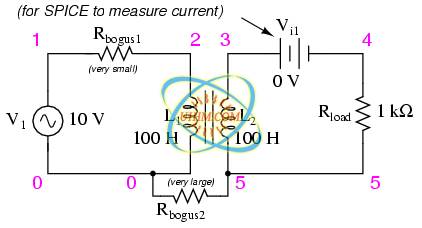
Spice circuit for coupled inductors.
transformer v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0 100 l2 3 5 100 ** This line tells SPICE that the two inductors ** l1 and l2 are magnetically “linked” together k l1 l2 0.999 vi1 3 4 ac 0 rload 4 5 1k .ac lin 1 60 60 .print ac v(2,0) i(v1) .print ac v(3,5) i(vi1) .end
Note: the Rbogus resistors are required to satisfy certain quirks of SPICE. The first breaks the otherwise continuous loop between the voltage source and L1 which would not be permitted by SPICE. The second provides a path to ground (node 0) from the secondary circuit, necessary because SPICE cannot function with any ungrounded circuits.
freq v(2) i(v1) 6.000E+01 1.000E+01 9.975E-03 Primary winding freq v(3,5) i(vi1) 6.000E+01 9.962E+00 9.962E-03 Secondary winding
Note that with equal inductances for both windings (100 Henrys each), the AC voltages and currents are nearly equal for the two. The difference between primary and secondary currents is the magnetizing current spoken of earlier: the 90o lagging current necessary to magnetize the core. As is seen here, it is usually very small compared to primary current induced by the load, and so the primary and secondary currents are almost equal. What you are seeing here is quite typical of transformer efficiency. Anything less than 95% efficiency is considered poor for modern power transformer designs, and this transfer of power occurs with no moving parts or other components subject to wear.
If we decrease the load resistance so as to draw more current with the same amount of voltage, we see that the current through the primary winding increases in response. Even though the AC power source is not directly connected to the load resistance (rather, it is electromagnetically “coupled”), the amount of current drawn from the source will be almost the same as the amount of current that would be drawn if the load were directly connected to the source. Take a close look at the next two SPICE simulations, showing what happens with different values of load resistors:
transformer v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0 100 l2 3 5 100 k l1 l2 0.999 vi1 3 4 ac 0 ** Note load resistance value of 200 ohms rload 4 5 200 .ac lin 1 60 60 .print ac v(2,0) i(v1) .print ac v(3,5) i(vi1) .end
freq v(2) i(v1) 6.000E+01 1.000E+01 4.679E-02 freq v(3,5) i(vi1) 6.000E+01 9.348E+00 4.674E-02
Notice how the primary current closely follows the secondary current. In our first simulation, both currents were approximately 10 mA, but now they are both around 47 mA. In this second simulation, the two currents are closer to equality, because the magnetizing current remains the same as before while the load current has increased. Note also how the secondary voltage has decreased some with the heavier (greater current) load. Let's try another simulation with an even lower value of load resistance (15 Ω):
transformer v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0 100 l2 3 5 100 k l1 l2 0.999 vi1 3 4 ac 0 rload 4 5 15 .ac lin 1 60 60 .print ac v(2,0) i(v1) .print ac v(3,5) i(vi1) .end
freq v(2) i(v1) 6.000E+01 1.000E+01 1.301E-01 freq v(3,5) i(vi1) 6.000E+01 1.950E+00 1.300E-01
Our load current is now 0.13 amps, or 130 mA, which is substantially higher than the last time. The primary current is very close to being the same, but notice how the secondary voltage has fallen well below the primary voltage (1.95 volts versus 10 volts at the primary). The reason for this is an imperfection in our transformer design: because the primary and secondary inductances aren't perfectly linked (a k factor of 0.999 instead of 1.000) there is “stray” or “leakage” inductance. In other words, some of the magnetic field isn't linking with the secondary coil, and thus cannot couple energy to it: (Figure below)
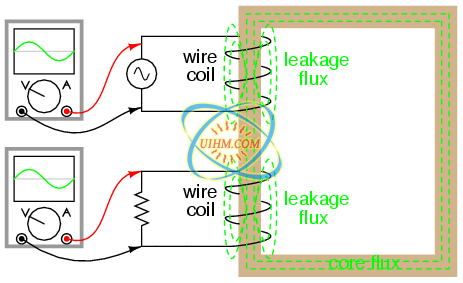
Leakage inductance is due to magnetic flux not cutting both windings.
Consequently, this “leakage” flux merely stores and returns energy to the source circuit via self-inductance, effectively acting as a series impedance in both primary and secondary circuits. Voltage gets dropped across this series impedance, resulting in a reduced load voltage: voltage across the load “sags” as load current increases. (Figure below)
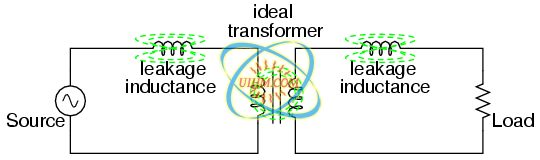
Equivalent circuit models leakage inductance as series inductors independent of the “ideal transformer”.
If we change the transformer design to have better magnetic coupling between the primary and secondary coils, the figures for voltage between primary and secondary windings will be much closer to equality again:
transformer v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0 100 l2 3 5 100 ** Coupling factor = 0.99999 instead of 0.999 k l1 l2 0.99999 vi1 3 4 ac 0 rload 4 5 15 .ac lin 1 60 60 .print ac v(2,0) i(v1) .print ac v(3,5) i(vi1) .end
freq v(2) i(v1) 6.000E+01 1.000E+01 6.658E-01 freq v(3,5) i(vi1) 6.000E+01 9.987E+00 6.658E-01
Here we see that our secondary voltage is back to being equal with the primary, and the secondary current is equal to the primary current as well. Unfortunately, building a real transformer with coupling this complete is very difficult. A compromise solution is to design both primary and secondary coils with less inductance, the strategy being that less inductance overall leads to less “leakage” inductance to cause trouble, for any given degree of magnetic coupling inefficiency. This results in a load voltage that is closer to ideal with the same (heavy) load and the same coupling factor:
transformer v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 ** inductance = 1 henry instead of 100 henrys l1 2 0 1 l2 3 5 1 k l1 l2 0.999 vi1 3 4 ac 0 rload 4 5 15 .ac lin 1 60 60 .print ac v(2,0) i(v1) .print ac v(3,5) i(vi1) .end
freq v(2) i(v1) 6.000E+01 1.000E+01 6.664E-01 freq v(3,5) i(vi1) 6.000E+01 9.977E+00 6.652E-01
Simply by using primary and secondary coils of less inductance, the load voltage for this heavy load has been brought back up to nearly ideal levels (9.977 volts). At this point, one might ask, “If less inductance is all that's needed to achieve near-ideal performance under heavy load, then why worry about coupling efficiency at all? If it's impossible to build a transformer with perfect coupling, but easy to design coils with low inductance, then why not just build all transformers with low-inductance coils and have excellent efficiency even with poor magnetic coupling?”
The answer to this question is found in another simulation: the same low-inductance transformer, but this time with a lighter load (1 kΩ instead of 15 Ω):
transformer v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0 1 l2 3 5 1 k l1 l2 0.999 vi1 3 4 ac 0 rload 4 5 1k .ac lin 1 60 60 .print ac v(2,0) i(v1) .print ac v(3,5) i(vi1) .end
freq v(2) i(v1) 6.000E+01 1.000E+01 2.835E-02 freq v(3,5) i(vi1) 6.000E+01 9.990E+00 9.990E-03
With lower winding inductances, the primary and secondary voltages are closer to being equal, but the primary and secondary currents are not. In this particular case, the primary current is 28.35 mA while the secondary current is only 9.990 mA: almost three times as much current in the primary as the secondary. Why is this? With less inductance in the primary winding, there is less inductive reactance, and consequently a much larger magnetizing current. A substantial amount of the current through the primary winding merely works to magnetize the core rather than transfer useful energy to the secondary winding and load.
An ideal transformer with identical primary and secondary windings would manifest equal voltage and current in both sets of windings for any load condition. In a perfect world, transformers would transfer electrical power from primary to secondary as smoothly as though the load were directly connected to the primary power source, with no transformer there at all. However, you can see this ideal goal can only be met if there is perfect coupling of magnetic flux between primary and secondary windings. Being that this is impossible to achieve, transformers must be designed to operate within certain expected ranges of voltages and loads in order to perform as close to ideal as possible. For now, the most important thing to keep in mind is a transformer's basic operating principle: the transfer of power from the primary to the secondary circuit via electromagnetic coupling.
- REVIEW:
- Mutual inductance is where the magnetic flux of two or more inductors are “linked” so that voltage is induced in one coil proportional to the rate-of-change of current in another.
- A transformer is a device made of two or more inductors, one of which is powered by AC, inducing an AC voltage across the second inductor. If the second inductor is connected to a load, power will be electromagnetically coupled from the first inductor's power source to that load.
- The powered inductor in a transformer is called the primary winding. The unpowered inductor in a transformer is called the secondary winding.
- Magnetic flux in the core (Φ) lags 90o behind the source voltage waveform. The current drawn by the primary coil from the source to produce this flux is called the magnetizing current, and it also lags the supply voltage by 90o.
- Total primary current in an unloaded transformer is called the exciting current, and is comprised of magnetizing current plus any additional current necessary to overcome core losses. It is never perfectly sinusoidal in a real transformer, but may be made more so if the transformer is designed and operated so that magnetic flux density is kept to a minimum.
- Core flux induces a voltage in any coil wrapped around the core. The induces voltage(s) are ideally in- phase with the primary winding source voltage and share the same waveshape.
- Any current drawn through the secondary winding by a load will be “reflected” to the primary winding and drawn from the voltage source, as if the source were directly powering a similar load.
Step-up and step-down transformers
So far, we've observed simulations of transformers where the primary and secondary windings were of identical inductance, giving approximately equal voltage and current levels in both circuits. Equality of voltage and current between the primary and secondary sides of a transformer, however, is not the norm for all transformers. If the inductances of the two windings are not equal, something interesting happens:
transformer v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0 10000 l2 3 5 100 k l1 l2 0.999 vi1 3 4 ac 0 rload 4 5 1k .ac lin 1 60 60 .print ac v(2,0) i(v1) .print ac v(3,5) i(vi1) .end
freq v(2) i(v1) 6.000E+01 1.000E+01 9.975E-05 Primary winding freq v(3,5) i(vi1) 6.000E+01 9.962E-01 9.962E-04 Secondary winding
Notice how the secondary voltage is approximately ten times less than the primary voltage (0.9962 volts compared to 10 volts), while the secondary current is approximately ten times greater (0.9962 mA compared to 0.09975 mA). What we have here is a device that steps voltage down by a factor of ten and current up by a factor of ten: (Figure below)
Turns ratio of 10:1 yields 10:1 primary:secondary voltage ratio and 1:10 primary:secondary current ratio.
This is a very useful device, indeed. With it, we can easily multiply or divide voltage and current in AC circuits. Indeed, the transformer has made long-distance transmission of electric power a practical reality, as AC voltage can be “stepped up” and current “stepped down” for reduced wire resistance power losses along power lines connecting generating stations with loads. At either end (both the generator and at the loads), voltage levels are reduced by transformers for safer operation and less expensive equipment. A transformer that increases voltage from primary to secondary (more secondary winding turns than primary winding turns) is called a step-up transformer. Conversely, a transformer designed to do just the opposite is called a step-down transformer.
Let's re-examine a photograph shown in the previous section: (Figure below)

Transformer cross-section showing primary and secondary windings is a few inches tall (approximately 10 cm).
This is a step-down transformer, as evidenced by the high turn count of the primary winding and the low turn count of the secondary. As a step-down unit, this transformer converts high-voltage, low-current power into low-voltage, high-current power. The larger-gauge wire used in the secondary winding is necessary due to the increase in current. The primary winding, which doesn't have to conduct as much current, may be made of smaller-gauge wire.
In case you were wondering, it is possible to operate either of these transformer types backwards (powering the secondary winding with an AC source and letting the primary winding power a load) to perform the opposite function: a step-up can function as a step-down and visa-versa. However, as we saw in the first section of this chapter, efficient operation of a transformer requires that the individual winding inductances be engineered for specific operating ranges of voltage and current, so if a transformer is to be used “backwards” like this it must be employed within the original design parameters of voltage and current for each winding, lest it prove to be inefficient (or lest it be damaged by excessive voltage or current!).
Transformers are often constructed in such a way that it is not obvious which wires lead to the primary winding and which lead to the secondary. One convention used in the electric power industry to help alleviate confusion is the use of “H” designations for the higher-voltage winding (the primary winding in a step-down unit; the secondary winding in a step-up) and “X” designations for the lower-voltage winding. Therefore, a simple power transformer will have wires labeled “H1”, “H2”, “X1”, and “X2”. There is usually significance to the numbering of the wires (H1 versus H2, etc.), which we'll explore a little later in this chapter.
The fact that voltage and current get “stepped” in opposite directions (one up, the other down) makes perfect sense when you recall that power is equal to voltage times current, and realize that transformers cannot produce power, only convert it. Any device that could output more power than it took in would violate the Law of Energy Conservation in physics, namely that energy cannot be created or destroyed, only converted. As with the first transformer example we looked at, power transfer efficiency is very good from the primary to the secondary sides of the device.
The practical significance of this is made more apparent when an alternative is considered: before the advent of efficient transformers, voltage/current level conversion could only be achieved through the use of motor/generator sets. A drawing of a motor/generator set reveals the basic principle involved: (Figure below)
Motor generator illustrates the basic principle of the transformer.
In such a machine, a motor is mechanically coupled to a generator, the generator designed to produce the desired levels of voltage and current at the rotating speed of the motor. While both motors and generators are fairly efficient devices, the use of both in this fashion compounds their inefficiencies so that the overall efficiency is in the range of 90% or less. Furthermore, because motor/generator sets obviously require moving parts, mechanical wear and balance are factors influencing both service life and performance. Transformers, on the other hand, are able to convert levels of AC voltage and current at very high efficiencies with no moving parts, making possible the widespread distribution and use of electric power we take for granted.
In all fairness it should be noted that motor/generator sets have not necessarily been obsoleted by transformers for all applications. While transformers are clearly superior over motor/generator sets for AC voltage and current level conversion, they cannot convert one frequency of AC power to another, or (by themselves) convert DC to AC or visa-versa. Motor/generator sets can do all these things with relative simplicity, albeit with the limitations of efficiency and mechanical factors already described. Motor/generator sets also have the unique property of kinetic energy storage: that is, if the motor's power supply is momentarily interrupted for any reason, its angular momentum (the inertia of that rotating mass) will maintain rotation of the generator for a short duration, thus isolating any loads powered by the generator from “glitches” in the main power system.
Looking closely at the numbers in the SPICE analysis, we should see a correspondence between the transformer's ratio and the two inductances. Notice how the primary inductor (l1) has 100 times more inductance than the secondary inductor (10000 H versus 100 H), and that the measured voltage step-down ratio was 10 to 1. The winding with more inductance will have higher voltage and less current than the other. Since the two inductors are wound around the same core material in the transformer (for the most efficient magnetic coupling between the two), the parameters affecting inductance for the two coils are equal except for the number of turns in each coil. If we take another look at our inductance formula, we see that inductance is proportional to the square of the number of coil turns:

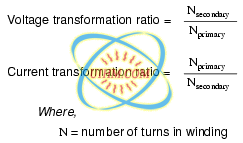
So, it should be apparent that our two inductors in the last SPICE transformer example circuit -- with inductance ratios of 100:1 -- should have coil turn ratios of 10:1, because 10 squared equals 100. This works out to be the same ratio we found between primary and secondary voltages and currents (10:1), so we can say as a rule that the voltage and current transformation ratio is equal to the ratio of winding turns between primary and secondary.
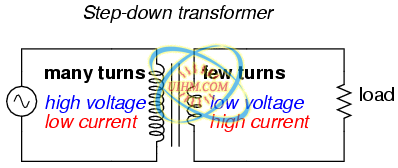
Step-down transformer: (many turns :few turns).
The step-up/step-down effect of coil turn ratios in a transformer (Figure above) is analogous to gear tooth ratios in mechanical gear systems, transforming values of speed and torque in much the same way: (Figure below)
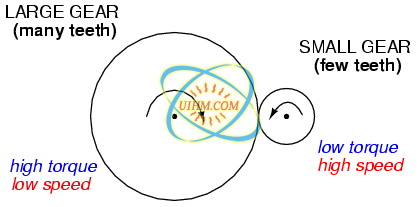
Torque reducing gear train steps torque down, while stepping speed up.
Step-up and step-down transformers for power distribution purposes can be gigantic in proportion to the power transformers previously shown, some units standing as tall as a home. The following photograph shows a substation transformer standing about twelve feet tall: (Figure below)

Substation transformer.
- REVIEW:
- Transformers “step up” or “step down” voltage according to the ratios of primary to secondary wire turns.
-
- A transformer designed to increase voltage from primary to secondary is called a step-up transformer. A transformer designed to reduce voltage from primary to secondary is called a step-down transformer.
- The transformation ratio of a transformer will be equal to the square root of its primary to secondary inductance (L) ratio.
-
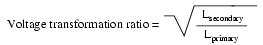
Electrical isolation
Aside from the ability to easily convert between different levels of voltage and current in AC and DC circuits, transformers also provide an extremely useful feature called isolation, which is the ability to couple one circuit to another without the use of direct wire connections. We can demonstrate an application of this effect with another SPICE simulation: this time showing “ground” connections for the two circuits, imposing a high DC voltage between one circuit and ground through the use of an additional voltage source:(Figure below)
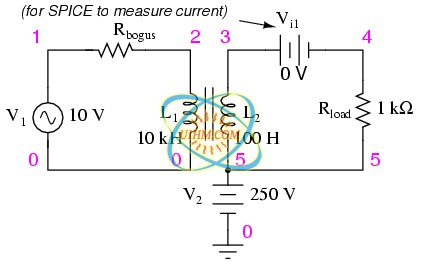
Transformer isolates 10 Vac at V1 from 250 VDC at V2.
v1 1 0 ac 10 sin rbogus1 1 2 1e-12 v2 5 0 dc 250 l1 2 0 10000 l2 3 5 100 k l1 l2 0.999 vi1 3 4 ac 0 rload 4 5 1k .ac lin 1 60 60 .print ac v(2,0) i(v1) .print ac v(3,5) i(vi1) .end
DC voltages referenced to ground (node 0): (1) 0.0000 (2) 0.0000 (3) 250.0000 (4) 250.0000 (5) 250.0000 AC voltages: freq v(2) i(v1) 6.000E+01 1.000E+01 9.975E-05 Primary winding freq v(3,5) i(vi1) 6.000E+01 9.962E-01 9.962E-04 Secondary winding
SPICE shows the 250 volts DC being impressed upon the secondary circuit elements with respect to ground, (Figure above) but as you can see there is no effect on the primary circuit (zero DC voltage) at nodes 1 and 2, and the transformation of AC power from primary to secondary circuits remains the same as before. The impressed voltage in this example is often called a common-mode voltage because it is seen at more than one point in the circuit with reference to the common point of ground. The transformer isolates the common-mode voltage so that it is not impressed upon the primary circuit at all, but rather isolated to the secondary side. For the record, it does not matter that the common-mode voltage is DC, either. It could be AC, even at a different frequency, and the transformer would isolate it from the primary circuit all the same.
There are applications where electrical isolation is needed between two AC circuit without any transformation of voltage or current levels. In these instances, transformers called isolation transformers having 1:1 transformation ratios are used. A benchtop isolation transformer is shown in Figure below.

Isolation transformer isolates power out from the power line.
- REVIEW:
- By being able to transfer power from one circuit to another without the use of interconnecting conductors between the two circuits, transformers provide the useful feature of electrical isolation.
- Transformers designed to provide electrical isolation without stepping voltage and current either up or down are called isolation transformers.
Phasing
Since transformers are essentially AC devices, we need to be aware of the phase relationships between the primary and secondary circuits. Using our SPICE example from before, we can plot the waveshapes (Figure below) for the primary and secondary circuits and see the phase relations for ourselves:
spice transient analysis file for use with nutmeg: transformer v1 1 0 sin(0 15 60 0 0) rbogus1 1 2 1e-12 v2 5 0 dc 250 l1 2 0 10000 l2 3 5 100 k l1 l2 0.999 vi1 3 4 ac 0 rload 4 5 1k .tran 0.5m 17m .end nutmeg commands: setplot tran1 plot v(2) v(3,5)
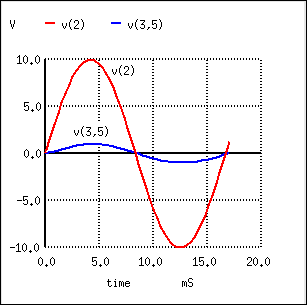
Secondary voltage V(3,5) is in-phase with primary voltage V(2), and stepped down by factor of ten.
In going from primary, V(2), to secondary, V(3,5), the voltage was stepped down by a factor of ten, (Figure above) , and the current was stepped up by a factor of 10. (Figure below) Both current (Figure below) and voltage (Figure above) waveforms are in-phase in going from primary to secondary.
nutmeg commands: setplot tran1 plot I(L1#branch) I(L2#branch)
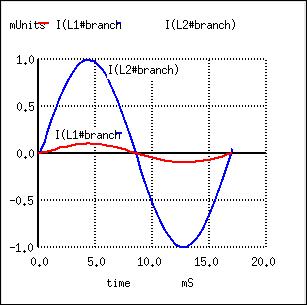
Primary and secondary currents are in-phase. Secondary current is stepped up by a factor of ten.
It would appear that both voltage and current for the two transformer windings are in-phase with each other, at least for our resistive load. This is simple enough, but it would be nice to know which way we should connect a transformer in order to ensure the proper phase relationships be kept. After all, a transformer is nothing more than a set of magnetically-linked inductors, and inductors don't usually come with polarity markings of any kind. If we were to look at an unmarked transformer, we would have no way of knowing which way to hook it up to a circuit to get in-phase (or 180o out-of-phase) voltage and current: (Figure below)

As a practical matter, the polarity of a transformer can be ambiguous.
Since this is a practical concern, transformer manufacturers have come up with a sort of polarity marking standard to denote phase relationships. It is called the dot convention, and is nothing more than a dot placed next to each corresponding leg of a transformer winding: (Figure below)
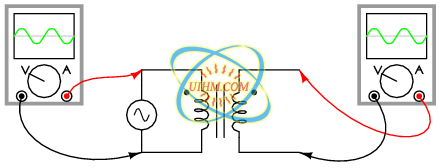
A pair of dots indicates like polarity.
Typically, the transformer will come with some kind of schematic diagram labeling the wire leads for primary and secondary windings. On the diagram will be a pair of dots similar to what is seen above. Sometimes dots will be omitted, but when “H” and “X” labels are used to label transformer winding wires, the subscript numbers are supposed to represent winding polarity. The “1” wires (H1 and X1) represent where the polarity-marking dots would normally be placed.
The similar placement of these dots next to the top ends of the primary and secondary windings tells us that whatever instantaneous voltage polarity seen across the primary winding will be the same as that across the secondary winding. In other words, the phase shift from primary to secondary will be zero degrees.
On the other hand, if the dots on each winding of the transformer do not match up, the phase shift will be 180o between primary and secondary, like this: (Figure below)
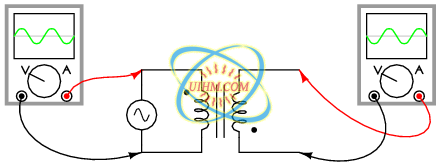
Out of phase: primary red to dot, secondary black to dot.
Of course, the dot convention only tells you which end of each winding is which, relative to the other winding(s). If you want to reverse the phase relationship yourself, all you have to do is swap the winding connections like this: (Figure below)
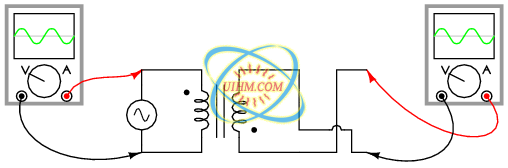
In phase: primary red to dot, secondary red to dot.
- REVIEW:
- The phase relationships for voltage and current between primary and secondary circuits of a transformer are direct: ideally, zero phase shift.
- The dot convention is a type of polarity marking for transformer windings showing which end of the winding is which, relative to the other windings.
Winding configurations
Transformers are very versatile devices. The basic concept of energy transfer between mutual inductors is useful enough between a single primary and single secondary coil, but transformers don't have to be made with just two sets of windings. Consider this transformer circuit: (Figure below)
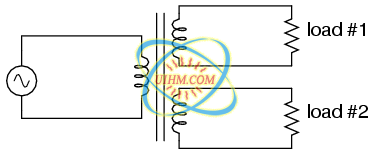
Transformer with multiple secondaries, provides multiple output voltages.
Here, three inductor coils share a common magnetic core, magnetically “coupling” or “linking” them together. The relationship of winding turn ratios and voltage ratios seen with a single pair of mutual inductors still holds true here for multiple pairs of coils. It is entirely possible to assemble a transformer such as the one above (one primary winding, two secondary windings) in which one secondary winding is a step-down and the other is a step-up. In fact, this design of transformer was quite common in vacuum tube power supply circuits, which were required to supply low voltage for the tubes' filaments (typically 6 or 12 volts) and high voltage for the tubes' plates (several hundred volts) from a nominal primary voltage of 110 volts AC. Not only are voltages and currents of completely different magnitudes possible with such a transformer, but all circuits are electrically isolated from one another.

Photograph of multiple-winding transformer with six windings, a primary and five secondaries.
The transformer in Figure above is intended to provide both high and low voltages necessary in an electronic system using vacuum tubes. Low voltage is required to power the filaments of vacuum tubes, while high voltage is required to create the potential difference between the plate and cathode elements of each tube. One transformer with multiple windings suffices elegantly to provide all the necessary voltage levels from a single 115 V source. The wires for this transformer (15 of them!) are not shown in the photograph, being hidden from view.
If electrical isolation between secondary circuits is not of great importance, a similar effect can be obtained by “tapping” a single secondary winding at multiple points along its length, like Figure below.
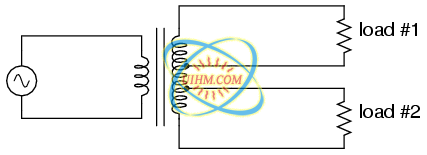
A single tapped secondary provides multiple voltages.
A tap is nothing more than a wire connection made at some point on a winding between the very ends. Not surprisingly, the winding turn/voltage magnitude relationship of a normal transformer holds true for all tapped segments of windings. This fact can be exploited to produce a transformer capable of multiple ratios: (Figure below)
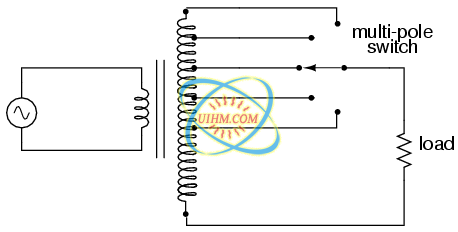
A tapped secondary using a switch to select one of many possible voltages.
Carrying the concept of winding taps further, we end up with a “variable transformer,” where a sliding contact is moved along the length of an exposed secondary winding, able to connect with it at any point along its length. The effect is equivalent to having a winding tap at every turn of the winding, and a switch with poles at every tap position: (Figure below)
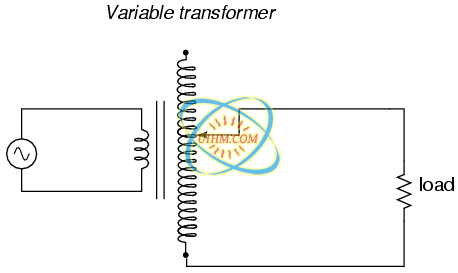
A sliding contact on the secondary continuously varies the secondary voltage.
One consumer application of the variable transformer is in speed controls for model train sets, especially the train sets of the 1950's and 1960's. These transformers were essentially step-down units, the highest voltage obtainable from the secondary winding being substantially less than the primary voltage of 110 to 120 volts AC. The variable-sweep contact provided a simple means of voltage control with little wasted power, much more efficient than control using a variable resistor!
Moving-slide contacts are too impractical to be used in large industrial power transformer designs, but multi-pole switches and winding taps are common for voltage adjustment. Adjustments need to be made periodically in power systems to accommodate changes in loads over months or years in time, and these switching circuits provide a convenient means. Typically, such “tap switches” are not engineered to handle full-load current, but must be actuated only when the transformer has been de-energized (no power).
Seeing as how we can tap any transformer winding to obtain the equivalent of several windings (albeit with loss of electrical isolation between them), it makes sense that it should be possible to forego electrical isolation altogether and build a transformer from a single winding. Indeed this is possible, and the resulting device is called an autotransformer: (Figure below)
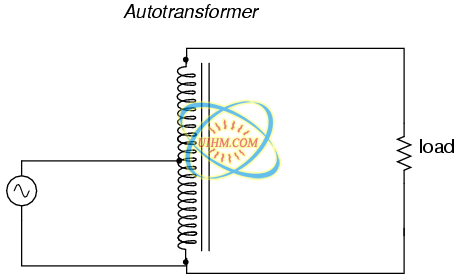
This autotransformer steps voltage up with a single tapped winding, saving copper, sacrificing isolation.
The autotransformer depicted above performs a voltage step-up function. A step-down autotransformer would look something like Figure below.
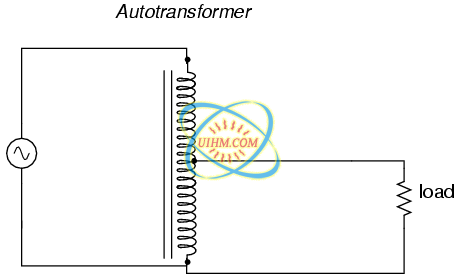
This auto transformer steps voltage down with a single copper-saving tapped winding.
Autotransformers find popular use in applications requiring a slight boost or reduction in voltage to a load. The alternative with a normal (isolated) transformer would be to either have just the right primary/secondary winding ratio made for the job or use a step-down configuration with the secondary winding connected in series-aiding (“boosting”) or series-opposing (“bucking”) fashion. Primary, secondary, and load voltages are given to illustrate how this would work.
First, the “boosting” configuration. In Figure below the secondary coil's polarity is oriented so that its voltage directly adds to the primary voltage.
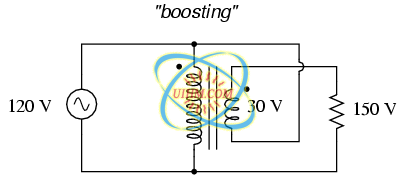
Ordinary transformer wired as an autotransformer to boost the line voltage.
Next, the “bucking” configuration. In Figure below the secondary coil's polarity is oriented so that its voltage directly subtracts from the primary voltage:
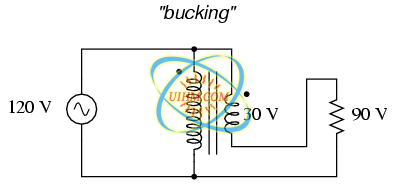
Ordinary transformer wired as an autotransformer to buck the line voltage down.
The prime advantage of an autotransformer is that the same boosting or bucking function is obtained with only a single winding, making it cheaper and lighter to manufacture than a regular (isolating) transformer having both primary and secondary windings.
Like regular transformers, autotransformer windings can be tapped to provide variations in ratio. Additionally, they can be made continuously variable with a sliding contact to tap the winding at any point along its length. The latter configuration is popular enough to have earned itself its own name: the Variac. (Figure below)
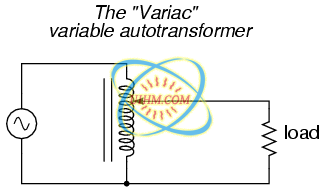
A variac is an autotransformer with a sliding tap.
Small variacs for benchtop use are popular pieces of equipment for the electronics experimenter, being able to step household AC voltage down (or sometimes up as well) with a wide, fine range of control by a simple twist of a knob.
- REVIEW:
- Transformers can be equipped with more than just a single primary and single secondary winding pair. This allows for multiple step-up and/or step-down ratios in the same device.
- Transformer windings can also be “tapped:” that is, intersected at many points to segment a single winding into sections.
- Variable transformers can be made by providing a movable arm that sweeps across the length of a winding, making contact with the winding at any point along its length. The winding, of course, has to be bare (no insulation) in the area where the arm sweeps.
- An autotransformer is a single, tapped inductor coil used to step up or step down voltage like a transformer, except without providing electrical isolation.
- A Variac is a variable autotransformer.
Voltage regulation
As we saw in a few SPICE analyses earlier in this chapter, the output voltage of a transformer varies some with varying load resistances, even with a constant voltage input. The degree of variance is affected by the primary and secondary winding inductances, among other factors, not the least of which includes winding resistance and the degree of mutual inductance (magnetic coupling) between the primary and secondary windings. For power transformer applications, where the transformer is seen by the load (ideally) as a constant source of voltage, it is good to have the secondary voltage vary as little as possible for wide variances in load current.
The measure of how well a power transformer maintains constant secondary voltage over a range of load currents is called the transformer's voltage regulation. It can be calculated from the following formula:
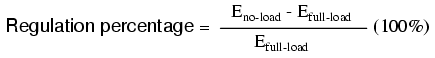
“Full-load” means the point at which the transformer is operating at maximum permissible secondary current. This operating point will be determined primarily by the winding wire size (ampacity) and the method of transformer cooling. Taking our first SPICE transformer simulation as an example, let's compare the output voltage with a 1 kΩ load versus a 200 Ω load (assuming that the 200 Ω load will be our “full load” condition). Recall if you will that our constant primary voltage was 10.00 volts AC:
freq v(3,5) i(vi1) 6.000E+01 9.962E+00 9.962E-03 Output with 1k ohm load freq v(3,5) i(vi1) 6.000E+01 9.348E+00 4.674E-02 Output with 200 ohm load
Notice how the output voltage decreases as the load gets heavier (more current). Now let's take that same transformer circuit and place a load resistance of extremely high magnitude across the secondary winding to simulate a “no-load” condition: (See "transformer" spice list")
transformer v1 1 0 ac 10 sin rbogus1 1 2 1e-12 rbogus2 5 0 9e12 l1 2 0 100 l2 3 5 100 k l1 l2 0.999 vi1 3 4 ac 0 rload 4 5 9e12 .ac lin 1 60 60 .print ac v(2,0) i(v1) .print ac v(3,5) i(vi1) .end
freq v(2) i(v1) 6.000E+01 1.000E+01 2.653E-04 freq v(3,5) i(vi1) 6.000E+01 9.990E+00 1.110E-12 Output with (almost) no load
So, we see that our output (secondary) voltage spans a range of 9.990 volts at (virtually) no load and 9.348 volts at the point we decided to call “full load.” Calculating voltage regulation with these figures, we get:
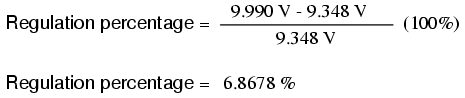
Incidentally, this would be considered rather poor (or “loose”) regulation for a power transformer. Powering a simple resistive load like this, a good power transformer should exhibit a regulation percentage of less than 3%. Inductive loads tend to create a condition of worse voltage regulation, so this analysis with purely resistive loads was a “best-case” condition.
There are some applications, however, where poor regulation is actually desired. One such case is in discharge lighting, where a step-up transformer is required to initially generate a high voltage (necessary to “ignite” the lamps), then the voltage is expected to drop off once the lamp begins to draw current. This is because discharge lamps' voltage requirements tend to be much lower after a current has been established through the arc path. In this case, a step-up transformer with poor voltage regulation suffices nicely for the task of conditioning power to the lamp.
Another application is in current control for AC arc welders, which are nothing more than step-down transformers supplying low-voltage, high-current power for the welding process. A high voltage is desired to assist in “striking” the arc (getting it started), but like the discharge lamp, an arc doesn't require as much voltage to sustain itself once the air has been heated to the point of ionization. Thus, a decrease of secondary voltage under high load current would be a good thing. Some arc welder designs provide arc current adjustment by means of a movable iron core in the transformer, cranked in or out of the winding assembly by the operator. Moving the iron slug away from the windings reduces the strength of magnetic coupling between the windings, which diminishes no-load secondary voltage and makes for poorer voltage regulation.
No exposition on transformer regulation could be called complete without mention of an unusual device called a ferroresonant transformer. “Ferroresonance” is a phenomenon associated with the behavior of iron cores while operating near a point of magnetic saturation (where the core is so strongly magnetized that further increases in winding current results in little or no increase in magnetic flux).
While being somewhat difficult to describe without going deep into electromagnetic theory, the ferroresonant transformer is a power transformer engineered to operate in a condition of persistent core saturation. That is, its iron core is “stuffed full” of magnetic lines of flux for a large portion of the AC cycle so that variations in supply voltage (primary winding current) have little effect on the core's magnetic flux density, which means the secondary winding outputs a nearly constant voltage despite significant variations in supply (primary winding) voltage. Normally, core saturation in a transformer results in distortion of the sinewave shape, and the ferroresonant transformer is no exception. To combat this side effect, ferroresonant transformers have an auxiliary secondary winding paralleled with one or more capacitors, forming a resonant circuit tuned to the power supply frequency. This “tank circuit” serves as a filter to reject harmonics created by the core saturation, and provides the added benefit of storing energy in the form of AC oscillations, which is available for sustaining output winding voltage for brief periods of input voltage loss (milliseconds' worth of time, but certainly better than nothing). (Figure below)
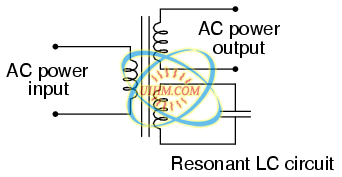
Ferroresonant transformer provides voltage regulation of the output.
In addition to blocking harmonics created by the saturated core, this resonant circuit also “filters out” harmonic frequencies generated by nonlinear (switching) loads in the secondary winding circuit and any harmonics present in the source voltage, providing “clean” power to the load.
Ferroresonant transformers offer several features useful in AC power conditioning: constant output voltage given substantial variations in input voltage, harmonic filtering between the power source and the load, and the ability to “ride through” brief losses in power by keeping a reserve of energy in its resonant tank circuit. These transformers are also highly tolerant of excessive loading and transient (momentary) voltage surges. They are so tolerant, in fact, that some may be briefly paralleled with unsynchronized AC power sources, allowing a load to be switched from one source of power to another in a “make-before-break” fashion with no interruption of power on the secondary side!
Unfortunately, these devices have equally noteworthy disadvantages: they waste a lot of energy (due to hysteresis losses in the saturated core), generating significant heat in the process, and are intolerant of frequency variations, which means they don't work very well when powered by small engine-driven generators having poor speed regulation. Voltages produced in the resonant winding/capacitor circuit tend to be very high, necessitating expensive capacitors and presenting the service technician with very dangerous working voltages. Some applications, though, may prioritize the ferroresonant transformer's advantages over its disadvantages. Semiconductor circuits exist to “condition” AC power as an alternative to ferroresonant devices, but none can compete with this transformer in terms of sheer simplicity.
- REVIEW:
- Voltage regulation is the measure of how well a power transformer can maintain constant secondary voltage given a constant primary voltage and wide variance in load current. The lower the percentage (closer to zero), the more stable the secondary voltage and the better the regulation it will provide.
- A ferroresonant transformer is a special transformer designed to regulate voltage at a stable level despite wide variation in input voltage.
Special transformers and applications
Impedance matching
Because transformers can step voltage and current to different levels, and because power is transferred equivalently between primary and secondary windings, they can be used to “convert” the impedance of a load to a different level. That last phrase deserves some explanation, so let's investigate what it means.
The purpose of a load (usually) is to do something productive with the power it dissipates. In the case of a resistive heating element, the practical purpose for the power dissipated is to heat something up. Loads are engineered to safely dissipate a certain maximum amount of power, but two loads of equal power rating are not necessarily identical. Consider these two 1000 watt resistive heating elements: (Figure below)

Heating elements dissipate 1000 watts, at different voltage and current ratings.
Both heaters dissipate exactly 1000 watts of power, but they do so at different voltage and current levels (either 250 volts and 4 amps, or 125 volts and 8 amps). Using Ohm's Law to determine the necessary resistance of these heating elements (R=E/I), we arrive at figures of 62.5 Ω and 15.625 Ω, respectively. If these are AC loads, we might refer to their opposition to current in terms of impedance rather than plain resistance, although in this case that's all they're composed of (no reactance). The 250 volt heater would be said to be a higher impedance load than the 125 volt heater.
If we desired to operate the 250 volt heater element directly on a 125 volt power system, we would end up being disappointed. With 62.5 Ω of impedance (resistance), the current would only be 2 amps (I=E/R; 125/62.5), and the power dissipation would only be 250 watts (P=IE; 125 x 2), or one-quarter of its rated power. The impedance of the heater and the voltage of our source would be mismatched, and we couldn't obtain the full rated power dissipation from the heater.
All hope is not lost, though. With a step-up transformer, we could operate the 250 volt heater element on the 125 volt power system like Figure below.
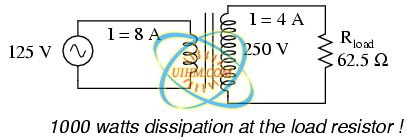
Step-up transformer operates 1000 watt 250 V heater from 125 V power source
The ratio of the transformer's windings provides the voltage step-up and current step-down we need for the otherwise mismatched load to operate properly on this system. Take a close look at the primary circuit figures: 125 volts at 8 amps. As far as the power supply “knows,” it's powering a 15.625 Ω (R=E/I) load at 125 volts, not a 62.5 Ω load! The voltage and current figures for the primary winding are indicative of 15.625 Ω load impedance, not the actual 62.5 Ω of the load itself. In other words, not only has our step-up transformer transformed voltage and current, but it has transformed impedance as well.
The transformation ratio of impedance is the square of the voltage/current transformation ratio, the same as the winding inductance ratio:
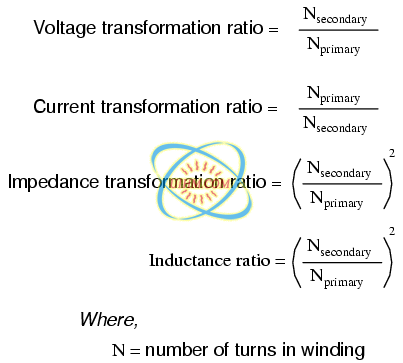
This concurs with our example of the 2:1 step-up transformer and the impedance ratio of 62.5 Ω to 15.625 Ω (a 4:1 ratio, which is 2:1 squared). Impedance transformation is a highly useful ability of transformers, for it allows a load to dissipate its full rated power even if the power system is not at the proper voltage to directly do so.
Recall from our study of network analysis the Maximum Power Transfer Theorem, which states that the maximum amount of power will be dissipated by a load resistance when that load resistance is equal to the Thevenin/Norton resistance of the network supplying the power. Substitute the word “impedance” for “resistance” in that definition and you have the AC version of that Theorem. If we're trying to obtain theoretical maximum power dissipation from a load, we must be able to properly match the load impedance and source (Thevenin/Norton) impedance together. This is generally more of a concern in specialized electric circuits such as radio transmitter/antenna and audio amplifier/speaker systems. Let's take an audio amplifier system and see how it works: (Figure below)
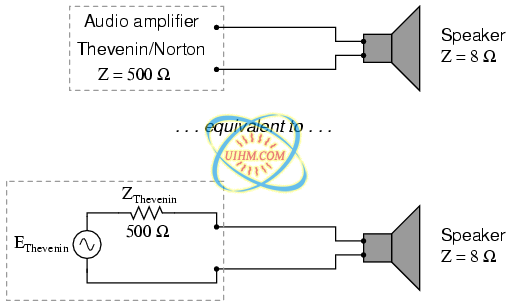
Amplifier with impedance of 500 Ω drives 8 Ω at much less than maximum power.
With an internal impedance of 500 Ω, the amplifier can only deliver full power to a load (speaker) also having 500 Ω of impedance. Such a load would drop higher voltage and draw less current than an 8 Ω speaker dissipating the same amount of power. If an 8 Ω speaker were connected directly to the 500 Ω amplifier as shown, the impedance mismatch would result in very poor (low peak power) performance. Additionally, the amplifier would tend to dissipate more than its fair share of power in the form of heat trying to drive the low impedance speaker.
To make this system work better, we can use a transformer to match these mismatched impedances. Since we're going from a high impedance (high voltage, low current) supply to a low impedance (low voltage, high current) load, we'll need to use a step-down transformer: (Figure below)
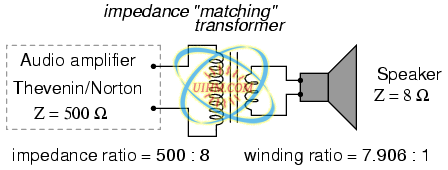
Impedance matching transformer matches 500 Ω amplifier to 8 Ω speaker for maximum efficiency.
To obtain an impedance transformation ratio of 500:8, we would need a winding ratio equal to the square root of 500:8 (the square root of 62.5:1, or 7.906:1). With such a transformer in place, the speaker will load the amplifier to just the right degree, drawing power at the correct voltage and current levels to satisfy the Maximum Power Transfer Theorem and make for the most efficient power delivery to the load. The use of a transformer in this capacity is called impedance matching.
Anyone who has ridden a multi-speed bicycle can intuitively understand the principle of impedance matching. A human's legs will produce maximum power when spinning the bicycle crank at a particular speed (about 60 to 90 revolution per minute). Above or below that rotational speed, human leg muscles are less efficient at generating power. The purpose of the bicycle's “gears” is to impedance-match the rider's legs to the riding conditions so that they always spin the crank at the optimum speed.
If the rider attempts to start moving while the bicycle is shifted into its “top” gear, he or she will find it very difficult to get moving. Is it because the rider is weak? No, it's because the high step-up ratio of the bicycle's chain and sprockets in that top gear presents a mismatch between the conditions (lots of inertia to overcome) and their legs (needing to spin at 60-90 RPM for maximum power output). On the other hand, selecting a gear that is too low will enable the rider to get moving immediately, but limit the top speed they will be able to attain. Again, is the lack of speed an indication of weakness in the bicyclist's legs? No, it's because the lower speed ratio of the selected gear creates another type of mismatch between the conditions (low load) and the rider's legs (losing power if spinning faster than 90 RPM). It is much the same with electric power sources and loads: there must be an impedance match for maximum system efficiency. In AC circuits, transformers perform the same matching function as the sprockets and chain (“gears”) on a bicycle to match otherwise mismatched sources and loads.
Impedance matching transformers are not fundamentally different from any other type of transformer in construction or appearance. A small impedance-matching transformer (about two centimeters in width) for audio-frequency applications is shown in the following photograph: (Figure below)

Audio frequency impedance matching transformer.
Another impedance-matching transformer can be seen on this printed circuit board, in the upper right corner, to the immediate left of resistors R2 and R1. It is labeled “T1”: (Figure below)

Printed circuit board mounted audio impedance matching transformer, top right.
Potential transformers
Transformers can also be used in electrical instrumentation systems. Due to transformers' ability to step up or step down voltage and current, and the electrical isolation they provide, they can serve as a way of connecting electrical instrumentation to high-voltage, high current power systems. Suppose we wanted to accurately measure the voltage of a 13.8 kV power system (a very common power distribution voltage in American industry): (Figure below)
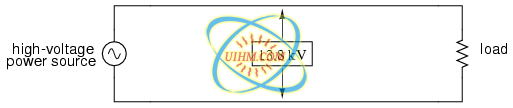
Direct measurement of high voltage by a voltmeter is a potential safety hazard.
Designing, installing, and maintaining a voltmeter capable of directly measuring 13,800 volts AC would be no easy task. The safety hazard alone of bringing 13.8 kV conductors into an instrument panel would be severe, not to mention the design of the voltmeter itself. However, by using a precision step-down transformer, we can reduce the 13.8 kV down to a safe level of voltage at a constant ratio, and isolate it from the instrument connections, adding an additional level of safety to the metering system: (Figure below)
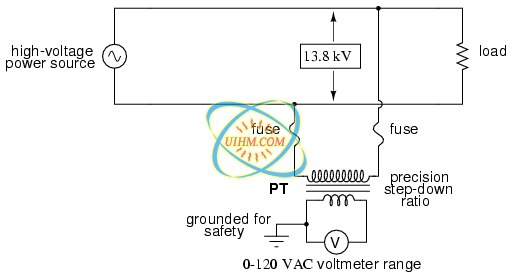
Instrumentation application:“Potential transformer” precisely scales dangerous high voltage to a safe value applicable to a conventional voltmeter.
Now the voltmeter reads a precise fraction, or ratio, of the actual system voltage, its scale set to read as though it were measuring the voltage directly. The transformer keeps the instrument voltage at a safe level and electrically isolates it from the power system, so there is no direct connection between the power lines and the instrument or instrument wiring. When used in this capacity, the transformer is called a Potential Transformer, or simply PT.
Potential transformers are designed to provide as accurate a voltage step-down ratio as possible. To aid in precise voltage regulation, loading is kept to a minimum: the voltmeter is made to have high input impedance so as to draw as little current from the PT as possible. As you can see, a fuse has been connected in series with the PTs primary winding, for safety and ease of disconnecting the PT from the circuit.
A standard secondary voltage for a PT is 120 volts AC, for full-rated power line voltage. The standard voltmeter range to accompany a PT is 150 volts, full-scale. PTs with custom winding ratios can be manufactured to suit any application. This lends itself well to industry standardization of the actual voltmeter instruments themselves, since the PT will be sized to step the system voltage down to this standard instrument level.
Current transformers
Following the same line of thinking, we can use a transformer to step down current through a power line so that we are able to safely and easily measure high system currents with inexpensive ammeters. Of course, such a transformer would be connected in series with the power line, like (Figure below).
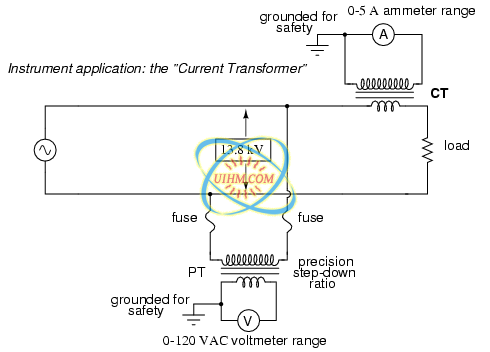
Instrumentation application: “Currrent transformer” steps high current down to a value applicable to a conventional ammeter.
Note that while the PT is a step-down device, the Current Transformer (or CT) is a step-up device (with respect to voltage), which is what is needed to step down the power line current. Quite often, CTs are built as donut-shaped devices through which the power line conductor is run, the power line itself acting as a single-turn primary winding: (Figure below)

Current conductor to be measured is threaded through the opening. Scaled down current is available on wire leads.
Some CTs are made to hinge open, allowing insertion around a power conductor without disturbing the conductor at all. The industry standard secondary current for a CT is a range of 0 to 5 amps AC. Like PTs, CTs can be made with custom winding ratios to fit almost any application. Because their “full load” secondary current is 5 amps, CT ratios are usually described in terms of full-load primary amps to 5 amps, like this:

The “donut” CT shown in the photograph has a ratio of 50:5. That is, when the conductor through the center of the torus is carrying 50 amps of current (AC), there will be 5 amps of current induced in the CT's winding.
Because CTs are designed to be powering ammeters, which are low-impedance loads, and they are wound as voltage step-up transformers, they should never, ever be operated with an open-circuited secondary winding. Failure to heed this warning will result in the CT producing extremely high secondary voltages, dangerous to equipment and personnel alike. To facilitate maintenance of ammeter instrumentation, short-circuiting switches are often installed in parallel with the CT's secondary winding, to be closed whenever the ammeter is removed for service: (Figure below)
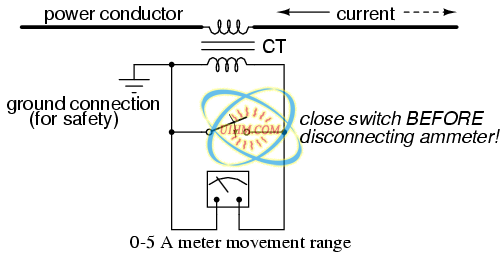
Short-circuit switch allows ammeter to be removed from an active current transformer circuit.
Though it may seem strange to intentionally short-circuit a power system component, it is perfectly proper and quite necessary when working with current transformers.
Air core transformers
Another kind of special transformer, seen often in radio-frequency circuits, is the air core transformer. (Figure below) True to its name, an air core transformer has its windings wrapped around a nonmagnetic form, usually a hollow tube of some material. The degree of coupling (mutual inductance) between windings in such a transformer is many times less than that of an equivalent iron-core transformer, but the undesirable characteristics of a ferromagnetic core (eddy current losses, hysteresis, saturation, etc.) are completely eliminated. It is in high-frequency applications that these effects of iron cores are most problematic.
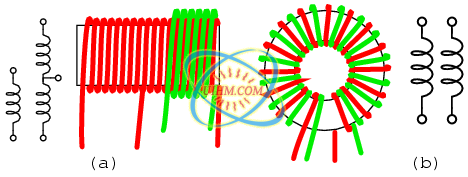
Air core transformers may be wound on cylindrical (a) or toroidal (b) forms. Center tapped primary with secondary (a). Bifilar winding on toroidal form (b).
The inside tapped solenoid winding, (Figure (a) above), without the over winding, could match unequal impedances when DC isolation is not required. When isolation is required the over winding is added over one end of the main winding. Air core transformers are used at radio frequencies when iron core losses are too high. Frequently air core transformers are paralleled with a capacitor to tune it to resonance. The over winding is connected between a radio antenna and ground for one such application. The secondary is tuned to resonance with a variable capacitor. The output may be taken from the tap point for amplification or detection. Small millimeter size air core transformers are used in radio receivers. The largest radio transmitters may use meter sized coils. Unshielded air core solenoid transformers are mounted at right angles to each other to prevent stray coupling.
Stray coupling is minimized when the transformer is wound on a toroid form. (Figure (b) above) Toroidal air core transformers also show a higher degree of coupling, particularly for bifilar windings. Bifilar windings are wound from a slightly twisted pair of wires. This implies a 1:1 turns ratio. Three or four wires may be grouped for 1:2 and other integral ratios. Windings do not have to be bifilar. This allows arbitrary turns ratios. However, the degree of coupling suffers. Toroidal air core transformers are rare except for VHF (Very High Frequency) work. Core materials other than air such as powdered iron or ferrite are preferred for lower radio frequencies.
Tesla Coil
One notable example of an air-core transformer is the Tesla Coil, named after the Serbian electrical genius Nikola Tesla, who was also the inventor of the rotating magnetic field AC motor, polyphase AC power systems, and many elements of radio technology. The Tesla Coil is a resonant, high-frequency step-up transformer used to produce extremely high voltages. One of Tesla's dreams was to employ his coil technology to distribute electric power without the need for wires, simply broadcasting it in the form of radio waves which could be received and conducted to loads by means of antennas. The basic schematic for a Tesla Coil is shown in Figure below.
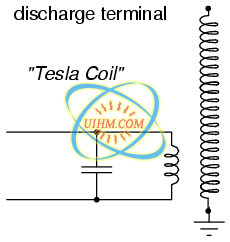
Tesla Coil: A few heavy primary turns, many secondary turns.
The capacitor, in conjunction with the transformer's primary winding, forms a tank circuit. The secondary winding is wound in close proximity to the primary, usually around the same nonmagnetic form. Several options exist for “exciting” the primary circuit, the simplest being a high-voltage, low-frequency AC source and spark gap: (Figure below)
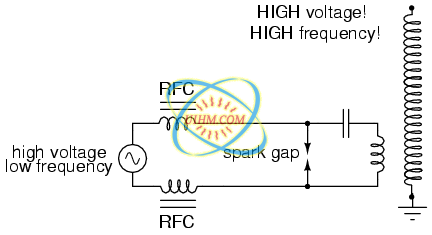
System level diagram of Tesla coil with spark gap drive.
The purpose of the high-voltage, low-frequency AC power source is to “charge” the primary tank circuit. When the spark gap fires, its low impedance acts to complete the capacitor/primary coil tank circuit, allowing it to oscillate at its resonant frequency. The “RFC” inductors are “Radio Frequency Chokes,” which act as high impedances to prevent the AC source from interfering with the oscillating tank circuit.
The secondary side of the Tesla coil transformer is also a tank circuit, relying on the parasitic (stray) capacitance existing between the discharge terminal and earth ground to complement the secondary winding's inductance. For optimum operation, this secondary tank circuit is tuned to the same resonant frequency as the primary circuit, with energy exchanged not only between capacitors and inductors during resonant oscillation, but also back-and-forth between primary and secondary windings. The visual results are spectacular: (Figure below)

High voltage high frequency discharge from Tesla coil.
Tesla Coils find application primarily as novelty devices, showing up in high school science fairs, basement workshops, and the occasional low budget science-fiction movie.
It should be noted that Tesla coils can be extremely dangerous devices. Burns caused by radio-frequency (“RF”) current, like all electrical burns, can be very deep, unlike skin burns caused by contact with hot objects or flames. Although the high-frequency discharge of a Tesla coil has the curious property of being beyond the “shock perception” frequency of the human nervous system, this does not mean Tesla coils cannot hurt or even kill you! I strongly advise seeking the assistance of an experienced Tesla coil experimenter if you would embark on building one yourself.
Saturable reactors
So far, we've explored the transformer as a device for converting different levels of voltage, current, and even impedance from one circuit to another. Now we'll take a look at it as a completely different kind of device: one that allows a small electrical signal to exert control over a much larger quantity of electrical power. In this mode, a transformer acts as an amplifier.
The device I'm referring to is called a saturable-core reactor, or simply saturable reactor. Actually, it is not really a transformer at all, but rather a special kind of inductor whose inductance can be varied by the application of a DC current through a second winding wound around the same iron core. Like the ferroresonant transformer, the saturable reactor relies on the principle of magnetic saturation. When a material such as iron is completely saturated (that is, all its magnetic domains are lined up with the applied magnetizing force), additional increases in current through the magnetizing winding will not result in further increases of magnetic flux.
Now, inductance is the measure of how well an inductor opposes changes in current by developing a voltage in an opposing direction. The ability of an inductor to generate this opposing voltage is directly connected with the change in magnetic flux inside the inductor resulting from the change in current, and the number of winding turns in the inductor. If an inductor has a saturated core, no further magnetic flux will result from further increases in current, and so there will be no voltage induced in opposition to the change in current. In other words, an inductor loses its inductance (ability to oppose changes in current) when its core becomes magnetically saturated.
If an inductor's inductance changes, then its reactance (and impedance) to AC current changes as well. In a circuit with a constant voltage source, this will result in a change in current: (Figure below)
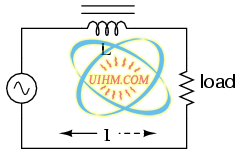
If L changes in inductance, ZL will correspondingly change, thus changing the circuit current.
A saturable reactor capitalizes on this effect by forcing the core into a state of saturation with a strong magnetic field generated by current through another winding. The reactor's “power” winding is the one carrying the AC load current, and the “control” winding is one carrying a DC current strong enough to drive the core into saturation: (Figure below)
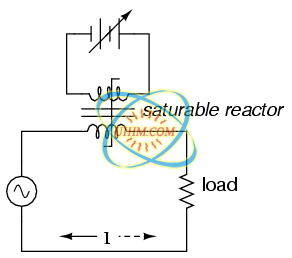
DC, via the control winding, saturates the core. Thus, modulating the power winding inductance, impedance, and current.
The strange-looking transformer symbol shown in the above schematic represents a saturable-core reactor, the upper winding being the DC control winding and the lower being the “power” winding through which the controlled AC current goes. Increased DC control current produces more magnetic flux in the reactor core, driving it closer to a condition of saturation, thus decreasing the power winding's inductance, decreasing its impedance, and increasing current to the load. Thus, the DC control current is able to exert control over the AC current delivered to the load.
The circuit shown would work, but it would not work very well. The first problem is the natural transformer action of the saturable reactor: AC current through the power winding will induce a voltage in the control winding, which may cause trouble for the DC power source. Also, saturable reactors tend to regulate AC power only in one direction: in one half of the AC cycle, the mmf's from both windings add; in the other half, they subtract. Thus, the core will have more flux in it during one half of the AC cycle than the other, and will saturate first in that cycle half, passing load current more easily in one direction than the other. Fortunately, both problems can be overcome with a little ingenuity: (Figure below)
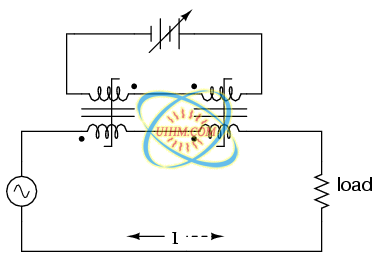
Out of phase DC control windings allow symmetrical of control AC.
Notice the placement of the phasing dots on the two reactors: the power windings are “in phase” while the control windings are “out of phase.” If both reactors are identical, any voltage induced in the control windings by load current through the power windings will cancel out to zero at the battery terminals, thus eliminating the first problem mentioned. Furthermore, since the DC control current through both reactors produces magnetic fluxes in different directions through the reactor cores, one reactor will saturate more in one cycle of the AC power while the other reactor will saturate more in the other, thus equalizing the control action through each half-cycle so that the AC power is “throttled” symmetrically. This phasing of control windings can be accomplished with two separate reactors as shown, or in a single reactor design with intelligent layout of the windings and core.
Saturable reactor technology has even been miniaturized to the circuit-board level in compact packages more generally known as magnetic amplifiers. I personally find this to be fascinating: the effect of amplification (one electrical signal controlling another), normally requiring the use of physically fragile vacuum tubes or electrically “fragile” semiconductor devices, can be realized in a device both physically and electrically rugged. Magnetic amplifiers do have disadvantages over their more fragile counterparts, namely size, weight, nonlinearity, and bandwidth (frequency response), but their utter simplicity still commands a certain degree of appreciation, if not practical application.
Saturable-core reactors are less commonly known as “saturable-core inductors” or transductors.
Scott-T transformer
Nikola Tesla's original polyphase power system was based on simple to build 2-phase components. However, as transmission distances increased, the more transmission line efficient 3-phase system became more prominent. Both 2-φ and 3-φ components coexisted for a number of years. The Scott-T transformer connection allowed 2-φ and 3-φ components like motors and alternators to be interconnected. Yamamoto and Yamaguchi:
In 1896, General Electric built a 35.5 km (22 mi) three-phase transmission line operated at 11 kV to transmit power to Buffalo, New York, from the Niagara Falls Project. The two-phase generated power was changed to three-phase by the use of Scott-T transformations. [MYA]
Scott-T transformer converts 2-φ to 3-φ, or vice versa.
The Scott-T transformer set, Figure above, consists of a center tapped transformer T1 and an 86.6% tapped transformer T2 on the 3-φ side of the circuit. The primaries of both transformers are connected to the 2-φ voltages. One end of the T2 86.6% secondary winding is a 3-φ output, the other end is connected to the T1 secondary center tap. Both ends of the T1 secondary are the other two 3-φ connections.
Application of 2-φ Niagara generator power produced a 3-φ output for the more efficient 3-φ transmission line. More common these days is the application of 3-φ power to produce a 2-φ output for driving an old 2-φ motor.
In Figure below, we use vectors in both polar and complex notation to prove that the Scott-T converts a pair of 2-φ voltages to 3-φ. First, one of the 3-φ voltages is identical to a 2-φ voltage due to the 1:1 transformer T1 ratio, VP12= V2P1. The T1 center tapped secondary produces opposite polarities of 0.5V2P1 on the secondary ends. This ∠0o is vectorially subtracted from T2 secondary voltage due to the KVL equations V31, V23. The T2 secondary voltage is 0.866V2P2 due to the 86.6% tap. Keep in mind that this 2nd phase of the 2-φ is ∠90o. This 0.866V2P2 is added at V31, subtracted at V23 in the KVL equations.
Scott-T transformer 2-φ to 3-φ conversion equations.
We show “DC” polarities all over this AC only circuit, to keep track of the Kirchhoff voltage loop polarities. Subtracting ∠0o is equivalent to adding ∠180o. The bottom line is when we add 86.6% of ∠90o to 50% of ∠180o we get ∠120o. Subtracting 86.6% of ∠90o from 50% of ∠180o yields ∠-120o or ∠240o.
Graphical explanation of equations in Figure previous.
In Figure above we graphically show the 2-φ vectors at (a). At (b) the vectors are scaled by transformers T1 and T2 to 0.5 and 0.866 respectively. At (c) 1∠120o = -0.5∠0o + 0.866∠90o, and 1∠240o = -0.5∠0o - 0.866∠90o. The three output phases are 1∠120o and 1∠240o from (c), along with input 1∠0o (a).
Linear Variable Differential Transformer
A linear variable differential transformer (LVDT) has an AC driven primary wound between two secondaries on a cylindrical air core form. (Figure below) A movable ferromagnetic slug converts displacement to a variable voltage by changing the coupling between the driven primary and secondary windings. The LVDT is a displacement or distance measuring transducer. Units are available for measuring displacement over a distance of a fraction of a millimeter to a half a meter. LVDT's are rugged and dirt resistant compared to linear optical encoders.
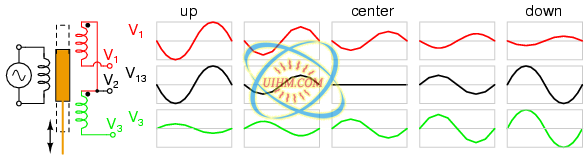
LVDT: linear variable differential transformer.
The excitation voltage is in the range of 0.5 to 10 VAC at a frequency of 1 to 200 Khz. A ferrite core is suitable at these frequencies. It is extended outside the body by an non-magnetic rod. As the core is moved toward the top winding, the voltage across this coil increases due to increased coupling, while the voltage on the bottom coil decreases. If the core is moved toward the bottom winding, the voltage on this coil increases as the voltage decreases across the top coil. Theoretically, a centered slug yields equal voltages across both coils. In practice leakage inductance prevents the null from dropping all the way to 0 V.
With a centered slug, the series-opposing wired secondaries cancel yielding V13 = 0. Moving the slug up increases V13. Note that it is in-phase with with V1, the top winding, and 180o out of phase with V2, bottom winding.
Moving the slug down from the center position increases V13. However, it is 180o out of phase with with V1, the top winding, and in-phase with V2, bottom winding. Moving the slug from top to bottom shows a minimum at the center point, with a 180o phase reversal in passing the center.
- REVIEW:
- Transformers can be used to transform impedance as well as voltage and current. When this is done to improve power transfer to a load, it is called impedance matching.
- A Potential Transformer (PT) is a special instrument transformer designed to provide a precise voltage step-down ratio for voltmeters measuring high power system voltages.
- A Current Transformer (CT) is another special instrument transformer designed to step down the current through a power line to a safe level for an ammeter to measure.
- An air-core transformer is one lacking a ferromagnetic core.
- A Tesla Coil is a resonant, air-core, step-up transformer designed to produce very high AC voltages at high frequency.
- A saturable reactor is a special type of inductor, the inductance of which can be controlled by the DC current through a second winding around the same core. With enough DC current, the magnetic core can be saturated, decreasing the inductance of the power winding in a controlled fashion.
- A Scott-T transformer converts 3-φ power to 2-φ power and vice versa.
- A linear variable differential transformer, also known as an LVDT, is a distance measuring device. It has a movable ferromagnetic core to vary the coupling between the excited primary and a pair of secondaries.
Practical considerations
Power capacity
As has already been observed, transformers must be well designed in order to achieve acceptable power coupling, tight voltage regulation, and low exciting current distortion. Also, transformers must be designed to carry the expected values of primary and secondary winding current without any trouble. This means the winding conductors must be made of the proper gauge wire to avoid any heating problems. An ideal transformer would have perfect coupling (no leakage inductance), perfect voltage regulation, perfectly sinusoidal exciting current, no hysteresis or eddy current losses, and wire thick enough to handle any amount of current. Unfortunately, the ideal transformer would have to be infinitely large and heavy to meet these design goals. Thus, in the business of practical transformer design, compromises must be made.
Additionally, winding conductor insulation is a concern where high voltages are encountered, as they often are in step-up and step-down power distribution transformers. Not only do the windings have to be well insulated from the iron core, but each winding has to be sufficiently insulated from the other in order to maintain electrical isolation between windings.
Respecting these limitations, transformers are rated for certain levels of primary and secondary winding voltage and current, though the current rating is usually derived from a volt-amp (VA) rating assigned to the transformer. For example, take a step-down transformer with a primary voltage rating of 120 volts, a secondary voltage rating of 48 volts, and a VA rating of 1 kVA (1000 VA). The maximum winding currents can be determined as such:

Sometimes windings will bear current ratings in amps, but this is typically seen on small transformers. Large transformers are almost always rated in terms of winding voltage and VA or kVA.
Energy losses
When transformers transfer power, they do so with a minimum of loss. As it was stated earlier, modern power transformer designs typically exceed 95% efficiency. It is good to know where some of this lost power goes, however, and what causes it to be lost.
There is, of course, power lost due to resistance of the wire windings. Unless superconducting wires are used, there will always be power dissipated in the form of heat through the resistance of current-carrying conductors. Because transformers require such long lengths of wire, this loss can be a significant factor. Increasing the gauge of the winding wire is one way to minimize this loss, but only with substantial increases in cost, size, and weight.
Resistive losses aside, the bulk of transformer power loss is due to magnetic effects in the core. Perhaps the most significant of these “core losses” is eddy-current loss, which is resistive power dissipation due to the passage of induced currents through the iron of the core. Because iron is a conductor of electricity as well as being an excellent “conductor” of magnetic flux, there will be currents induced in the iron just as there are currents induced in the secondary windings from the alternating magnetic field. These induced currents -- as described by the perpendicularity clause of Faraday's Law -- tend to circulate through the cross-section of the core perpendicularly to the primary winding turns. Their circular motion gives them their unusual name: like eddies in a stream of water that circulate rather than move in straight lines.
Iron is a fair conductor of electricity, but not as good as the copper or aluminum from which wire windings are typically made. Consequently, these “eddy currents” must overcome significant electrical resistance as they circulate through the core. In overcoming the resistance offered by the iron, they dissipate power in the form of heat. Hence, we have a source of inefficiency in the transformer that is difficult to eliminate.
This phenomenon is so pronounced that it is often exploited as a means of heating ferrous (iron-containing) materials. The photograph of (Figure below) shows an “induction heating” unit raising the temperature of a large pipe section. Loops of wire covered by high-temperature insulation encircle the pipe's circumference, inducing eddy currents within the pipe wall by electromagnetic induction. In order to maximize the eddy current effect, high-frequency alternating current is used rather than power line frequency (60 Hz). The box units at the right of the picture produce the high-frequency AC and control the amount of current in the wires to stabilize the pipe temperature at a pre-determined “set-point.”

Induction heating: Primary insulated winding induces current into lossy iron pipe (secondary).
The main strategy in mitigating these wasteful eddy currents in transformer cores is to form the iron core in sheets, each sheet covered with an insulating varnish so that the core is divided up into thin slices. The result is very little width in the core for eddy currents to circulate in: (Figure below)
Dividing the iron core into thin insulated laminations minimizes eddy current loss.
Laminated cores like the one shown here are standard in almost all low-frequency transformers. Recall from the photograph of the transformer cut in half that the iron core was composed of many thin sheets rather than one solid piece. Eddy current losses increase with frequency, so transformers designed to run on higher-frequency power (such as 400 Hz, used in many military and aircraft applications) must use thinner laminations to keep the losses down to a respectable minimum. This has the undesirable effect of increasing the manufacturing cost of the transformer.
Another, similar technique for minimizing eddy current losses which works better for high-frequency applications is to make the core out of iron powder instead of thin iron sheets. Like the lamination sheets, these granules of iron are individually coated in an electrically insulating material, which makes the core nonconductive except for within the width of each granule. Powdered iron cores are often found in transformers handling radio-frequency currents.
Another “core loss” is that of magnetic hysteresis. All ferromagnetic materials tend to retain some degree of magnetization after exposure to an external magnetic field. This tendency to stay magnetized is called “hysteresis,” and it takes a certain investment in energy to overcome this opposition to change every time the magnetic field produced by the primary winding changes polarity (twice per AC cycle). This type of loss can be mitigated through good core material selection (choosing a core alloy with low hysteresis, as evidenced by a “thin” B/H hysteresis curve), and designing the core for minimum flux density (large cross-sectional area).
Transformer energy losses tend to worsen with increasing frequency. The skin effect within winding conductors reduces the available cross-sectional area for electron flow, thereby increasing effective resistance as the frequency goes up and creating more power lost through resistive dissipation. Magnetic core losses are also exaggerated with higher frequencies, eddy currents and hysteresis effects becoming more severe. For this reason, transformers of significant size are designed to operate efficiently in a limited range of frequencies. In most power distribution systems where the line frequency is very stable, one would think excessive frequency would never pose a problem. Unfortunately it does, in the form of harmonics created by nonlinear loads.
As we've seen in earlier chapters, nonsinusoidal waveforms are equivalent to additive series of multiple sinusoidal waveforms at different amplitudes and frequencies. In power systems, these other frequencies are whole-number multiples of the fundamental (line) frequency, meaning that they will always be higher, not lower, than the design frequency of the transformer. In significant measure, they can cause severe transformer overheating. Power transformers can be engineered to handle certain levels of power system harmonics, and this capability is sometimes denoted with a “K factor” rating.
Stray capacitance and inductance
Aside from power ratings and power losses, transformers often harbor other undesirable limitations which circuit designers must be made aware of. Like their simpler counterparts -- inductors -- transformers exhibit capacitance due to the insulation dielectric between conductors: from winding to winding, turn to turn (in a single winding), and winding to core. Usually this capacitance is of no concern in a power application, but small signal applications (especially those of high frequency) may not tolerate this quirk well. Also, the effect of having capacitance along with the windings' designed inductance gives transformers the ability to resonate at a particular frequency, definitely a design concern in signal applications where the applied frequency may reach this point (usually the resonant frequency of a power transformer is well beyond the frequency of the AC power it was designed to operate on).
Flux containment (making sure a transformer's magnetic flux doesn't escape so as to interfere with another device, and making sure other devices' magnetic flux is shielded from the transformer core) is another concern shared both by inductors and transformers.
Closely related to the issue of flux containment is leakage inductance. We've already seen the detrimental effects of leakage inductance on voltage regulation with SPICE simulations early in this chapter. Because leakage inductance is equivalent to an inductance connected in series with the transformer's winding, it manifests itself as a series impedance with the load. Thus, the more current drawn by the load, the less voltage available at the secondary winding terminals. Usually, good voltage regulation is desired in transformer design, but there are exceptional applications. As was stated before, discharge lighting circuits require a step-up transformer with “loose” (poor) voltage regulation to ensure reduced voltage after the establishment of an arc through the lamp. One way to meet this design criterion is to engineer the transformer with flux leakage paths for magnetic flux to bypass the secondary winding(s). The resulting leakage flux will produce leakage inductance, which will in turn produce the poor regulation needed for discharge lighting.
Core saturation
Transformers are also constrained in their performance by the magnetic flux limitations of the core. For ferromagnetic core transformers, we must be mindful of the saturation limits of the core. Remember that ferromagnetic materials cannot support infinite magnetic flux densities: they tend to “saturate” at a certain level (dictated by the material and core dimensions), meaning that further increases in magnetic field force (mmf) do not result in proportional increases in magnetic field flux (Φ).
When a transformer's primary winding is overloaded from excessive applied voltage, the core flux may reach saturation levels during peak moments of the AC sinewave cycle. If this happens, the voltage induced in the secondary winding will no longer match the wave-shape as the voltage powering the primary coil. In other words, the overloaded transformer will distort the waveshape from primary to secondary windings, creating harmonics in the secondary winding's output. As we discussed before, harmonic content in AC power systems typically causes problems.
Special transformers known as peaking transformers exploit this principle to produce brief voltage pulses near the peaks of the source voltage waveform. The core is designed to saturate quickly and sharply, at voltage levels well below peak. This results in a severely cropped sine-wave flux waveform, and secondary voltage pulses only when the flux is changing (below saturation levels): (Figure below)
Voltage and flux waveforms for a peaking transformer.
Another cause of abnormal transformer core saturation is operation at frequencies lower than normal. For example, if a power transformer designed to operate at 60 Hz is forced to operate at 50 Hz instead, the flux must reach greater peak levels than before in order to produce the same opposing voltage needed to balance against the source voltage. This is true even if the source voltage is the same as before. (Figure below)
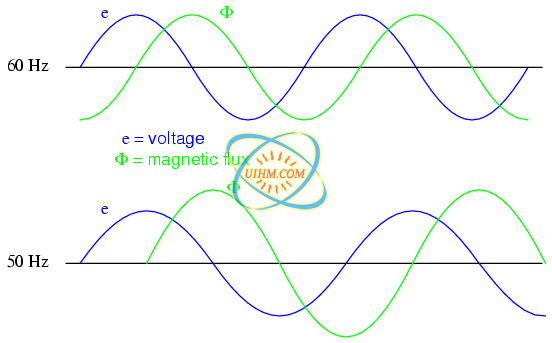
Magnetic flux is higher in a transformer core driven by 50 Hz as compared to 60 Hz for the same voltage.
Since instantaneous winding voltage is proportional to the instantaneous magnetic flux's rate of change in a transformer, a voltage waveform reaching the same peak value, but taking a longer amount of time to complete each half-cycle, demands that the flux maintain the same rate of change as before, but for longer periods of time. Thus, if the flux has to climb at the same rate as before, but for longer periods of time, it will climb to a greater peak value. (Figure below)
Mathematically, this is another example of calculus in action. Because the voltage is proportional to the flux's rate-of-change, we say that the voltage waveform is the derivative of the flux waveform, “derivative” being that calculus operation defining one mathematical function (waveform) in terms of the rate-of-change of another. If we take the opposite perspective, though, and relate the original waveform to its derivative, we may call the original waveform the integral of the derivative waveform. In this case, the voltage waveform is the derivative of the flux waveform, and the flux waveform is the integral of the voltage waveform.
The integral of any mathematical function is proportional to the area accumulated underneath the curve of that function. Since each half-cycle of the 50 Hz waveform accumulates more area between it and the zero line of the graph than the 60 Hz waveform will -- and we know that the magnetic flux is the integral of the voltage -- the flux will attain higher values in Figure below.
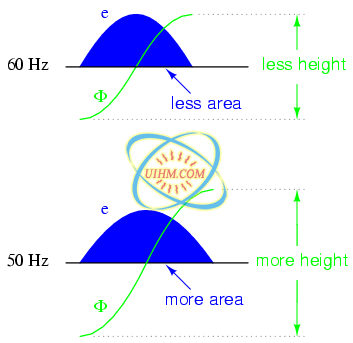
Flux changing at the same rate rises to a higher level at 50 Hz than at 60 Hz.
Yet another cause of transformer saturation is the presence of DC current in the primary winding. Any amount of DC voltage dropped across the primary winding of a transformer will cause additional magnetic flux in the core. This additional flux “bias” or “offset” will push the alternating flux waveform closer to saturation in one half-cycle than the other. (Figure below)
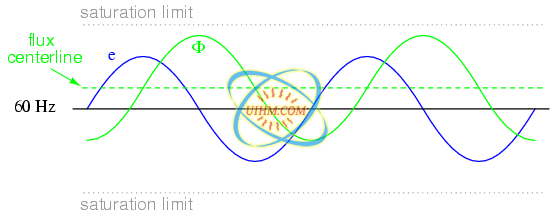
DC in primary, shifts the waveform peaks toward the upper saturation limit.
For most transformers, core saturation is a very undesirable effect, and it is avoided through good design: engineering the windings and core so that magnetic flux densities remain well below the saturation levels. This ensures that the relationship between mmf and Φ is more linear throughout the flux cycle, which is good because it makes for less distortion in the magnetization current waveform. Also, engineering the core for low flux densities provides a safe margin between the normal flux peaks and the core saturation limits to accommodate occasional, abnormal conditions such as frequency variation and DC offset.
Inrush current
When a transformer is initially connected to a source of AC voltage, there may be a substantial surge of current through the primary winding called inrush current. (Figure below) This is analogous to the inrush current exhibited by an electric motor that is started up by sudden connection to a power source, although transformer inrush is caused by a different phenomenon.
We know that the rate of change of instantaneous flux in a transformer core is proportional to the instantaneous voltage drop across the primary winding. Or, as stated before, the voltage waveform is the derivative of the flux waveform, and the flux waveform is the integral of the voltage waveform. In a continuously-operating transformer, these two waveforms are phase-shifted by 90o. (Figure below) Since flux (Φ) is proportional to the magnetomotive force (mmf) in the core, and the mmf is proportional to winding current, the current waveform will be in-phase with the flux waveform, and both will be lagging the voltage waveform by 90o:

Continuous steady-state operation: Magnetic flux, like current, lags applied voltage by 90o.
Let us suppose that the primary winding of a transformer is suddenly connected to an AC voltage source at the exact moment in time when the instantaneous voltage is at its positive peak value. In order for the transformer to create an opposing voltage drop to balance against this applied source voltage, a magnetic flux of rapidly increasing value must be generated. The result is that winding current increases rapidly, but actually no more rapidly than under normal conditions: (Figure below)
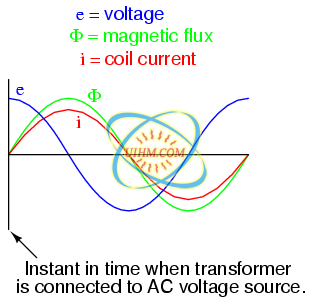
Connecting transformer to line at AC volt peak: Flux increases rapidly from zero, same as steady-state operation.
Both core flux and coil current start from zero and build up to the same peak values experienced during continuous operation. Thus, there is no “surge” or “inrush” or current in this scenario. (Figure above)
Alternatively, let us consider what happens if the transformer's connection to the AC voltage source occurs at the exact moment in time when the instantaneous voltage is at zero. During continuous operation (when the transformer has been powered for quite some time), this is the point in time where both flux and winding current are at their negative peaks, experiencing zero rate-of-change (dΦ/dt = 0 and di/dt = 0). As the voltage builds to its positive peak, the flux and current waveforms build to their maximum positive rates-of-change, and on upward to their positive peaks as the voltage descends to a level of zero:
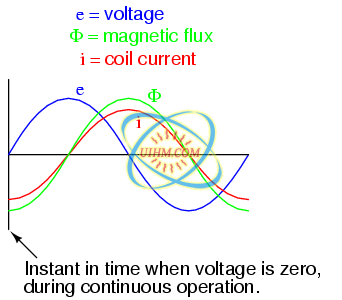
Starting at e=0 V is not the same as running continuously in Figure above. These expected waveforms are incorrect-- Φ and i should start at zero.
A significant difference exists, however, between continuous-mode operation and the sudden starting condition assumed in this scenario: during continuous operation, the flux and current levels were at their negative peaks when voltage was at its zero point; in a transformer that has been sitting idle, however, both magnetic flux and winding current should start at zero. When the magnetic flux increases in response to a rising voltage, it will increase from zero upward, not from a previously negative (magnetized) condition as we would normally have in a transformer that's been powered for awhile. Thus, in a transformer that's just “starting,” the flux will reach approximately twice its normal peak magnitude as it “integrates” the area under the voltage waveform's first half-cycle: (Figure below)
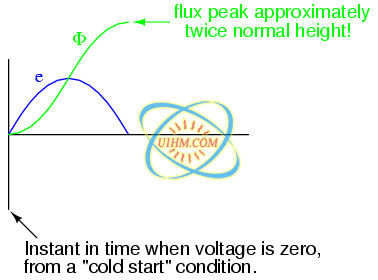
Starting at e=0 V, Φ starts at initial condition Φ=0, increasing to twice the normal value, assuming it doesn't saturate the core.
In an ideal transformer, the magnetizing current would rise to approximately twice its normal peak value as well, generating the necessary mmf to create this higher-than-normal flux. However, most transformers aren't designed with enough of a margin between normal flux peaks and the saturation limits to avoid saturating in a condition like this, and so the core will almost certainly saturate during this first half-cycle of voltage. During saturation, disproportionate amounts of mmf are needed to generate magnetic flux. This means that winding current, which creates the mmf to cause flux in the core, will disproportionately rise to a value easily exceeding twice its normal peak: (Figure below)
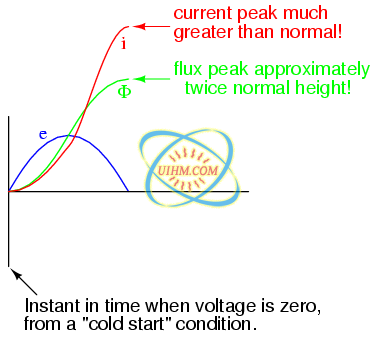
Starting at e=0 V, Current also increases to twice the normal value for an unsaturated core, or considerably higher in the (designed for) case of saturation.
This is the mechanism causing inrush current in a transformer's primary winding when connected to an AC voltage source. As you can see, the magnitude of the inrush current strongly depends on the exact time that electrical connection to the source is made. If the transformer happens to have some residual magnetism in its core at the moment of connection to the source, the inrush could be even more severe. Because of this, transformer overcurrent protection devices are usually of the “slow-acting” variety, so as to tolerate current surges such as this without opening the circuit.
Heat and Noise
In addition to unwanted electrical effects, transformers may also exhibit undesirable physical effects, the most notable being the production of heat and noise. Noise is primarily a nuisance effect, but heat is a potentially serious problem because winding insulation will be damaged if allowed to overheat. Heating may be minimized by good design, ensuring that the core does not approach saturation levels, that eddy currents are minimized, and that the windings are not overloaded or operated too close to maximum ampacity.
Large power transformers have their core and windings submerged in an oil bath to transfer heat and muffle noise, and also to displace moisture which would otherwise compromise the integrity of the winding insulation. Heat-dissipating “radiator” tubes on the outside of the transformer case provide a convective oil flow path to transfer heat from the transformer's core to ambient air: (Figure below)
Large power transformers are submerged in heat dissipating insulating oil.
Oil-less, or “dry,” transformers are often rated in terms of maximum operating temperature “rise” (temperature increase beyond ambient) according to a letter-class system: A, B, F, or H. These letter codes are arranged in order of lowest heat tolerance to highest:
- Class A: No more than 55o Celsius winding temperature rise, at 40o Celsius (maximum) ambient air temperature.
- Class B: No more than 80o Celsius winding temperature rise, at 40o Celsius (maximum)ambient air temperature.
- Class F: No more than 115o Celsius winding temperature rise, at 40o Celsius (maximum)ambient air temperature.
- Class H: No more than 150o Celsius winding temperature rise, at 40o Celsius (maximum)ambient air temperature.
Audible noise is an effect primarily originating from the phenomenon of magnetostriction: the slight change of length exhibited by a ferromagnetic object when magnetized. The familiar “hum” heard around large power transformers is the sound of the iron core expanding and contracting at 120 Hz (twice the system frequency, which is 60 Hz in the United States) -- one cycle of core contraction and expansion for every peak of the magnetic flux waveform -- plus noise created by mechanical forces between primary and secondary windings. Again, maintaining low magnetic flux levels in the core is the key to minimizing this effect, which explains why ferroresonant transformers -- which must operate in saturation for a large portion of the current waveform -- operate both hot and noisy.
Another noise-producing phenomenon in power transformers is the physical reaction force between primary and secondary windings when heavily loaded. If the secondary winding is open-circuited, there will be no current through it, and consequently no magneto-motive force (mmf) produced by it. However, when the secondary is “loaded” (current supplied to a load), the winding generates an mmf, which becomes counteracted by a “reflected” mmf in the primary winding to prevent core flux levels from changing. These opposing mmf's generated between primary and secondary windings as a result of secondary (load) current produce a repulsive, physical force between the windings which will tend to make them vibrate. Transformer designers have to consider these physical forces in the construction of the winding coils, to ensure there is adequate mechanical support to handle the stresses. Under heavy load conditions, though, these stresses may be great enough to cause audible noise to emanate from the transformer.
- REVIEW:
- Power transformers are limited in the amount of power they can transfer from primary to secondary winding(s). Large units are typically rated in VA (volt-amps) or kVA (kilo volt-amps).
- Resistance in transformer windings contributes to inefficiency, as current will dissipate heat, wasting energy.
- Magnetic effects in a transformer's iron core also contribute to inefficiency. Among the effects are eddy currents (circulating induction currents in the iron core) and hysteresis (power lost due to overcoming the tendency of iron to magnetize in a particular direction).
- Increased frequency results in increased power losses within a power transformer. The presence of harmonics in a power system is a source of frequencies significantly higher than normal, which may cause overheating in large transformers.
- Both transformers and inductors harbor certain unavoidable amounts of capacitance due to wire insulation (dielectric) separating winding turns from the iron core and from each other. This capacitance can be significant enough to give the transformer a natural resonant frequency, which can be problematic in signal applications.
- Leakage inductance is caused by magnetic flux not being 100% coupled between windings in a transformer. Any flux not involved with transferring energy from one winding to another will store and release energy, which is how (self-) inductance works. Leakage inductance tends to worsen a transformer's voltage regulation (secondary voltage “sags” more for a given amount of load current).
- Magnetic saturation of a transformer core may be caused by excessive primary voltage, operation at too low of a frequency, and/or by the presence of a DC current in any of the windings. Saturation may be minimized or avoided by conservative design, which provides an adequate margin of safety between peak magnetic flux density values and the saturation limits of the core.
- Transformers often experience significant inrush currents when initially connected to an AC voltage source. Inrush current is most severe when connection to the AC source is made at the moment instantaneous source voltage is zero.
- Noise is a common phenomenon exhibited by transformers -- especially power transformers -- and is primarily caused by magnetostriction of the core. Physical forces causing winding vibration may also generate noise under conditions of heavy (high current) secondary winding load.
Hot
temperature curve of induction thermal treatment after welding 600MW turbine valve
Main Circuit of UM DSP air cooled induction heaters
what is skin effect principle (magnetic force around induction coil)
How to design an optimal induction coil
Applications of induction heating
History of induction heating
what is induction welding
whate is induction tempering or induction preheating






Newest Comment
No Comment
Post Comment